
科目: 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.
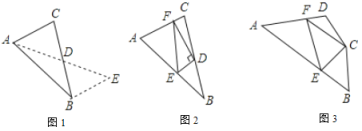
(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】一服装批发店出售某品牌童装,每件进价120元,批发价200元,多买优惠;凡是一次买10件以上的,每多买一件,所买的全部服装每件就降低1元,但是最低价为为每件160元,
(1)求一次至少买多少件,才能以最低价购买?
(2)写出服装店一次销售x件时,获利润y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲批发了46件,乙批发了50件,店主却发现卖46件赚的钱反而比卖50件赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, AB 是 ⊙ O 的直径, C 是![]() 的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
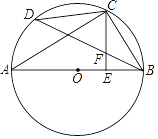
(1)求证: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形 ABCD 中, AC 平分 ∠ DAB , ∠ ADC= ∠ ACB=90° , E 为 AB 的中点,连接 CE , DE . AC 与 DE 相交于点 F .
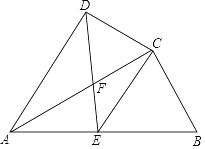
(1)求证: △ ADF ∽△ CEF ;
(2)若 AD=4 , AB=6 ,求 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小高发现电线杆 AB 的影子落在土坡的坡面CD和地面 BC上,量得 CD= 12 米 , BC= 20 米 ,CD与地面成30°角,且此时测得1米杆的影长为2 米,求电线杆的高度.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,![]() 与
与 ![]() 是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
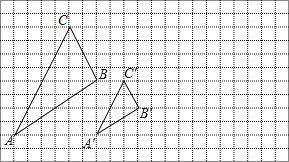
![]() 画出位似中心点O;
画出位似中心点O;
![]() 直接写出
直接写出![]() 与
与![]() 的位似比;
的位似比;
![]() 以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出
以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出![]() 各顶点的坐标.
各顶点的坐标.
查看答案和解析>>
科目: 来源: 题型:
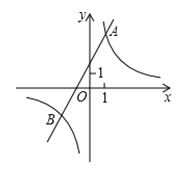
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
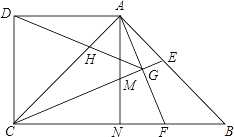
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
查看答案和解析>>
科目: 来源: 题型:
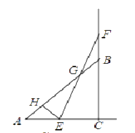
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
A.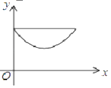 B.
B.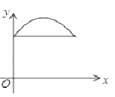 C.
C.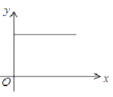 D.
D.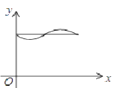
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上 ,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上 ,称为二次变换,……经过连续2017次变换后,顶点A的坐标是:

A. (4033, ![]() ) B. (4033,0) C. (4036,
) B. (4033,0) C. (4036, ![]() ) D. (4036,0)
) D. (4036,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com