
科目: 来源: 题型:
【题目】如图点![]() 分别是边长为4cm的等边三角形
分别是边长为4cm的等边三角形![]() 边
边![]() 动点,点
动点,点![]() 从顶点
从顶点![]() 沿
沿![]() 向点
向点![]() 运动,点
运动,点![]() 同时从顶点
同时从顶点![]() 沿
沿![]() 向
向![]() 运动,它们的速度都是
运动,它们的速度都是![]() ,当到达终点时停止运动,设运动时间为t秒,连接
,当到达终点时停止运动,设运动时间为t秒,连接![]() 交于点M.
交于点M.
(1)求证:![]() ;
;
(2)点![]() 在运动的过程中,
在运动的过程中,![]() 变化吗?若变化,请说明理由,若不变,则求出它的度数;
变化吗?若变化,请说明理由,若不变,则求出它的度数;
(3)当![]() 为何值时
为何值时![]() 是直角三角形?
是直角三角形?

查看答案和解析>>
科目: 来源: 题型:
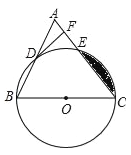
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
科目: 来源: 题型:
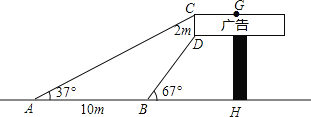
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】近两年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信.B支付宝.C银行卡.D其他.该小组选取了某一超市一天之内购买者的支付方式进行统计,得到如下两幅不完整的统计图.
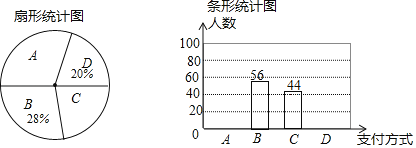
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名购买者?
(2)补全条形统计图:“A微信”支付方式所在扇形的圆心角为 度;
(3)若该超市这一天内有2000名购买者,请你估计B种支付方式的购买者有多少人?
查看答案和解析>>
科目: 来源: 题型:
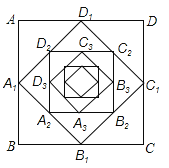
【题目】连接正方形四边的中点所构成的正方形,我们称其原正方形的中点正方形,如图,已知正方形![]() 的中点正方形
的中点正方形![]() ,再作正方形
,再作正方形![]() 的中点正方形
的中点正方形![]() ,这样不断下去,第n次所做的中点正方形
,这样不断下去,第n次所做的中点正方形![]() ,若正方形
,若正方形![]() 的边长为1,若设中点正方形
的边长为1,若设中点正方形![]() 的面积为
的面积为![]() ,则
,则![]() ___________.
___________.
查看答案和解析>>
科目: 来源: 题型:
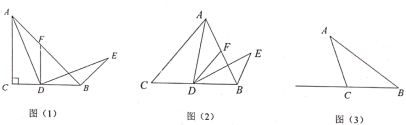
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
A.5B.4C.3D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,其对称轴与抛物线交于点
,其对称轴与抛物线交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 为抛物线对称轴上的一个动点,从点
为抛物线对称轴上的一个动点,从点![]() 出发,沿射线
出发,沿射线![]() 以每秒2个单位长度的速度运动,过点
以每秒2个单位长度的速度运动,过点![]() 作
作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边).设点
的左边).设点![]() 的运动时间为
的运动时间为![]() .
.
①当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
②连接![]() ,在点
,在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标:若不存在,请说明理由;
的坐标:若不存在,请说明理由;
③点![]() 在
在![]() 轴上,点
轴上,点![]() 为坐标平面内一点,以线段
为坐标平面内一点,以线段![]() 为对角线作菱形
为对角线作菱形![]() ,当
,当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
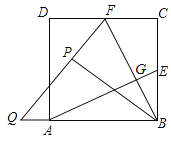
【题目】综合与实践
(1)(探索发现)在![]() 中.
中. ![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
如图(1),当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,试猜想:
时,试猜想:
①![]() 与
与![]() 之间的数量关系:______;
之间的数量关系:______;
②![]() ______.
______.
(2)(拓展探究)
如图(2),当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,判断
时,判断![]() 与
与![]() 之间的数量关系及
之间的数量关系及![]() 的度数,请说明理由.
的度数,请说明理由.
(3)(解决问题)
如图(3),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
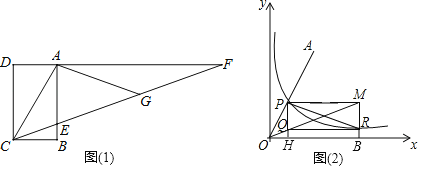
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com