
科目: 来源: 题型:
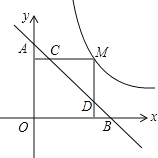
【题目】如图,点M为双曲线y=![]() 上一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+2m于D、C两点,若直线y=﹣x+2m交y轴于A,交x轴于B,则ADBC的值为_____.
上一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+2m于D、C两点,若直线y=﹣x+2m交y轴于A,交x轴于B,则ADBC的值为_____.
查看答案和解析>>
科目: 来源: 题型:
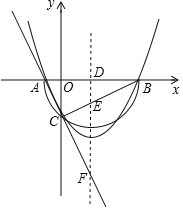
【题目】已知二次函数y=x2+bx+c+1的图象与x轴交于点A(x1,0)、B(x2,0),且x1<x2,与y轴的负半轴交于点C.
(1)当b=1时,求c的取值范围;
(2)如果以AB为直径的半圆恰好过点C,求c的值;
(3)在(2)的条件下,如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F,且满足DE=2EF,求二次函数的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[m﹣1,m+1,﹣2m]的函数的一些结论,其中不正确的是( )
A.当m=2时,函数图象的顶点坐标为![]()
B.当m>1时,函数图象截x轴所得的线段长大于3
C.当m<0时,函数在x<![]() 时,y随x的增大而增大
时,y随x的增大而增大
D.不论m取何值,函数图象经过两个定点
查看答案和解析>>
科目: 来源: 题型:
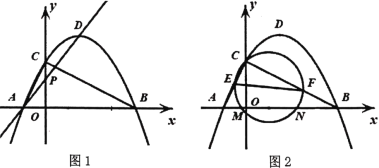
【题目】如图![]() ,二次函数
,二次函数![]() (
(![]() 、
、![]() 为参数,其中
为参数,其中![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)若![]() ,求
,求![]() 的值(结果用含
的值(结果用含![]() 的式子表示);
的式子表示);
(2)若![]() 是等腰三角形,直线
是等腰三角形,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() .求抛物线的解析式;
.求抛物线的解析式;
(3)如图![]() ,已知
,已知![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,并交
,并交![]() 轴于
轴于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
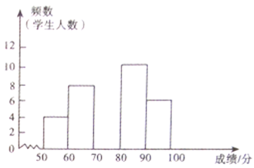
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com