
科目: 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段,下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳远(米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳绳(次) | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A.5号学生进入30秒跳绳决赛
B.2号学生进入30秒跳绳决赛
C.8号学生进入30秒跳绳决赛
D.9号学生进入30秒跳绳决赛
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 的图象经过
的图象经过![]() ,与y轴交于点C,抛物线
,与y轴交于点C,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),交直线
与x轴交于点A,B(点A在点B的左侧),交直线![]() 于点P.
于点P.
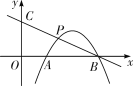
(1)若![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)若点P是线段![]() 的中点,求a的值;
的中点,求a的值;
(3)设点P的横坐标为![]() ,则当
,则当![]() 时,直接写出此时a的取值范围.
时,直接写出此时a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数![]() 的图象
的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)当![]() 的顶点在
的顶点在![]() 上时,求
上时,求![]() 的值;
的值;
(2)若![]() 、
、![]() 两点中有一点与点
两点中有一点与点![]() 关于原点对称,试判断这个点是点
关于原点对称,试判断这个点是点![]() 还是点
还是点![]() ;
;
(3)若![]() 的顶点为
的顶点为![]() ,对称轴与
,对称轴与![]() 的交点为
的交点为![]() ,且点
,且点![]() 在点
在点![]() 的下方,当
的下方,当![]() 为何值时,线段
为何值时,线段![]() 的长最大.
的长最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 的对称轴交于点
的对称轴交于点![]() ,与
,与![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() .
.
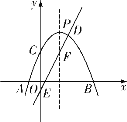
(1)求![]() 的值;
的值;
(2)点![]() 能否与点
能否与点![]() 关于
关于![]() 轴的对称点重合?若认为能,请求出
轴的对称点重合?若认为能,请求出![]() 的值;若认为不能,说明理由;
的值;若认为不能,说明理由;
(3)小林研究了抛物线![]() 的解析式后,得到了如下的结论:因为
的解析式后,得到了如下的结论:因为![]() 可以取任意实数,所以点
可以取任意实数,所以点![]() 可以在
可以在![]() 轴上任意移动,即
轴上任意移动,即![]() 点可以到达
点可以到达![]() 轴的任何位置,你认为他说的有道理吗?说说你的理由;
轴的任何位置,你认为他说的有道理吗?说说你的理由;
(4)当抛物线![]() 与直线
与直线![]() 有两个公共点时,直接写出适合条件的
有两个公共点时,直接写出适合条件的![]() 的最大整数.
的最大整数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(﹣3,3),过点A的直线y=![]() x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
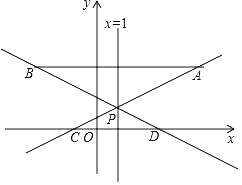
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)定义“![]() 双抛图形”:直线
双抛图形”:直线![]() 将抛物线
将抛物线![]() 分成两部分,首先去掉其不含顶点的部分,然后作出抛物线剩余部分关于直线
分成两部分,首先去掉其不含顶点的部分,然后作出抛物线剩余部分关于直线![]() 的对称图形,得到的整个图形称为抛物线
的对称图形,得到的整个图形称为抛物线![]() 关于直线
关于直线![]() 的“
的“![]() 双抛图形”(特别地,当直线
双抛图形”(特别地,当直线![]() 恰好是抛物线的对称轴时,得到的“
恰好是抛物线的对称轴时,得到的“![]() 双抛图形”不变).
双抛图形”不变).
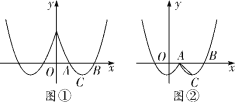
①当![]() 时,抛物线
时,抛物线![]() 关于直线
关于直线![]() 的“
的“![]() 双抛图形”如图①所示,直线
双抛图形”如图①所示,直线![]() 与“
与“![]() 双抛图形”有________个交点;
双抛图形”有________个交点;
②若抛物线![]() 关于直线
关于直线![]() 的“
的“![]() 双抛图形”与直线
双抛图形”与直线![]() 恰好有两个交点,结合图象,直接写出
恰好有两个交点,结合图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 的坐标是
的坐标是![]() ,抛物线
,抛物线![]() 经过原点
经过原点![]() 和点
和点![]() ,已知正方形
,已知正方形![]() 的三个顶点为
的三个顶点为![]() ,
,![]() ,
,![]() .
.
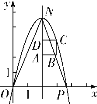
(1)若当![]() 时,求
时,求![]() ,
,![]() ,并写出抛物线对称轴及
,并写出抛物线对称轴及![]() 的最大值;
的最大值;
(2)求证:抛物线的顶点在函数![]() 的图象上;
的图象上;
(3)若抛物线与直线![]() 交于点
交于点![]() ,求
,求![]() 为何值时,
为何值时,![]() 的面积为1;
的面积为1;
(4)若抛物线经过正方形区域![]() (含边界),请直接写出
(含边界),请直接写出![]() 的取值范围.
的取值范围.
(参考公式:![]() 的顶点坐标是
的顶点坐标是 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A,B两点,且A点在B的右侧.
(1)当抛物线经过点(3,8),求a的值;
(2)求A、B两点的坐标;
(3)若抛物线的顶点为M,且点M到x轴的距离等于AB的3倍,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=![]() .
.
(1)若反比例函数y=![]() (x>0)的图象经过AO的中点C,求k的值;
(x>0)的图象经过AO的中点C,求k的值;
(2)在(1)的条件下,若反比例函数y=![]() (x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(3)若点D关于y轴的对称点为E,当反比例函数y=![]() 的图象和线段AE有公共点时,直接写出k的取值范围.
的图象和线段AE有公共点时,直接写出k的取值范围.
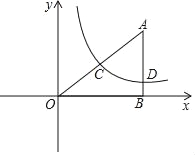
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com