练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．设等比数列{an}的公比|q|＞1，前n项和为Sn，已知a3=2，S4=5S2，求a5+a7．

    分析 利用等比数列的求和公式及S4=5S2化简可知（1-q2）（1+q2）=5（1-q2），进而可知公比q=2，计算即得结论；

    解答 解：由等比数列{an}的公比|q|＞1，S4=5S2，得$\frac{{a}_{1}（1-{q}^{4}）}{1-q}$=5•$\frac{{a}_{1}（1-{q}^{2}）}{1-q}$，
    即（1-q2）（1+q2）=5（1-q2），
    因为|q|＞1，所以1-q2≠0，
    从而1+q2=5，从而q=2，a3=2，
    于是an=a3qn-2=2n-1；
    a5+a7=24+26=80．

    点评 本题考查数列的通项及前n项和，考查运算求解能力，注意解题方法的积累，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．（1）已知sinx-cosx=$\frac{1}{3}$，求sin4x+cos4x的值；
    （2）已知sinx+cosx=-$\frac{7}{13}$（0＜x＜π），求cosx-2sinx的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如图中的三个直角三角形是一个体积为35cm3的几何体的三视图，则侧视图中的h（　　）
    A．5cmB．6cmC．7cmD．8cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在△ABC中，D为BC的中点，O在AD上且AO=$\frac{1}{4}$AD，AB=2，AC=6，则$\overrightarrow{BC}$•$\overrightarrow{AO}$等于4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=（　　）
    A．$\sqrt{2}$B．$\sqrt{5}$C．$\sqrt{3}$D．$\sqrt{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．六名同学排在一起照相，其中甲、乙两人必须分开的不同排法有（　　）
    A．480种B．360种C．240种D．120种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

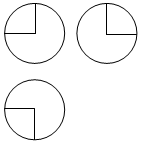    10．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是$\frac{28π}{3}$，则它的表面积是（　　）
    A．17πB．18πC．20πD．28π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．等差数列{an}中，a3+a4=4，a5+a7=6．
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在平面直角坐标系xOy中，双曲线$\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{3}$=1的焦距是2$\sqrt{10}$．

    查看答案和解析>>

    同步练习册答案