
分析 作出函数f(x)=max(sinx,cosx)的图象,然后逐一核对六个命题得答案.
解答 解:画出函数y=f(x)=max(sinx,cosx)的图象如图所示: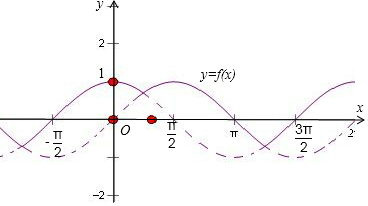
由图可知:
①f(x)的定义域是R,故①正确;
②函数f(x)的值域为[-$\frac{\sqrt{2}}{2}$,1],故②错误;
③f(x)的图象不关于原点中心对称,f(x)不是奇函数,故③错误;
④x=2kπ或2kπ+$\frac{π}{2}$,k∈Z时,f(x)的最大值是1,故④正确;
⑤函数f(x)是最小正周期为2π的函数,故⑤正确;
⑥f(x)的递增区间是[2kπ+$\frac{π}{4}$,2kπ+$\frac{π}{2}$],[2kπ+$\frac{5π}{4}$,2kπ+2π],k∈Z,故⑥错误.
综上,正确的命题序号是①④⑤.
故答案为:①④⑤.
点评 本题考查了分段函数的定义、图象与性质的应用问题,也考查了画图与识图的能力,是中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (5,+∞) | C. | (-∞,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )
如图,1,2,3,4号是四盏灯,A、B、C是控制这四盏灯的三个开关,若开关A控制2,3,4号灯(即按一下开关A,2,3,4号四盏灯亮,再按一下开关A,2,3,4号四盏灯熄灭),开关B控制1,3,4号灯,开关C控制1,2,4号灯.开始时,四盏灯都亮着,那么下面的说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 实数不是复数 | B. | 3+i的共轭复数是-3-i | ||
| C. | 1+$\sqrt{3}i$不是纯虚数 | D. | z$\overline{z}$=z2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com