
分析 (1 )先根据二倍角公式化简,再根据f(x)图象的一个对称中心为点,即可求出答案,
(2)先根据余弦定理求出C的值,再求出A,根据两角和的正弦公式即可求出.
解答 解:f(x)=cos2(x-φ)-sin2(x-φ)=cos(2x-2φ)
(1)由题知:2×$\frac{π}{3}$-2φ=$\frac{π}{2}$+kπ,解得 $2φ=\frac{π}{6}-kπ$
又$φ∈({0,\frac{π}{2}})$,
故$2φ=\frac{π}{6}$即$φ=\frac{π}{12}$;
(2)由a2+b2-c2=ab得$cosc=\frac{1}{2}$,
解得$c=\frac{π}{3}$,
又$({\frac{A}{2}+\frac{π}{12}})=\frac{{\sqrt{2}}}{2}$,
故$cos({A+\frac{π}{6}-\frac{π}{6}})=\frac{{\sqrt{2}}}{2}$,
解得$A=\frac{π}{4}$,
故$B=π-A-C=π-({\frac{π}{3}+\frac{π}{4}})$,
$sinB=sin({\frac{π}{3}+\frac{π}{4}})=\frac{{\sqrt{2}}}{2}-\frac{{1+\sqrt{3}}}{2}=\frac{{\sqrt{6}+\sqrt{2}}}{4}$.
点评 本题考查了三角函数的化简和以及三角函数的图象和性质,属于中档题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:解答题
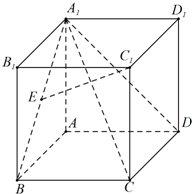 如图长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4,E为BA1的中点.
如图长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4,E为BA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)f(-x)是偶函数 | B. | f(x)|f(-x)|是奇函数 | C. | f(x)-f(-x)是偶函数 | D. | f(x)+f(-x)是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com