
分析 (1)根据偶函数的定义得xlog2(ax+$\sqrt{a{x^2}+b}$)=-xlog2(-ax+$\sqrt{a{x^2}+b}$);
(2)把不等式$\frac{{\sqrt{3}}}{3}$f(x-2)<log2(2+$\sqrt{3}$)转化为f(x-2)<$\sqrt{3}$log2(2+$\sqrt{3}$)=f($\sqrt{3}$),得f(|x-2|)<f($\sqrt{3}$),即|x-2|<$\sqrt{3}$解得即可.
解答 解:(Ⅰ)由已知得xlog2(ax+$\sqrt{a{x^2}+b}$)=-xlog2(-ax+$\sqrt{a{x^2}+b}$),即xlog2(ax+$\sqrt{a{x^2}+b}$)=0
∴$\left\{\begin{array}{l}{a={a}^{2}}\\{b=1}\end{array}\right.$,∴$\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$(舍去)或$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$,
当a=1,b=1时,满足f(x)是偶函数,故a=1,b=1.(6分)
(Ⅱ)由(Ⅰ)知f(x)=xlog2(x+$\sqrt{{x^2}+1}$),
显然在x∈(0,+∞)上f(x)是增函数,
$\frac{{\sqrt{3}}}{3}$f(x-2)<log2(2+$\sqrt{3}$)?f(x-2)<$\sqrt{3}$log2(2+$\sqrt{3}$)=f($\sqrt{3}$),
∵f(-x)=f(x)=f(|x|),
∴f(|x-2|)<f($\sqrt{3}$),|x-2|<$\sqrt{3}$,
∴x∈(2-$\sqrt{3}$,2+$\sqrt{3}$).(12分)
点评 本题主要考查函数的奇偶性和不等式,属于中等题.


科目:高中数学 来源: 题型:选择题
| A. | 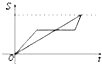 | B. | 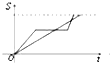 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
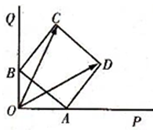 如图,边长为2的正方形ABCD的顶点A,B分别在两条互相垂直的射线OP,OQ上滑动,则$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值为8.
如图,边长为2的正方形ABCD的顶点A,B分别在两条互相垂直的射线OP,OQ上滑动,则$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{89}{2}$ | B. | 61 | C. | 39 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com