
| A. | 当a=2时,x=1是f(x)的一个极值点 | B. | 当-2<a<2时,函数f(x)无极值 | ||
| C. | 当a>2时,f(x)的极小值小于0 | D. | ?a∈R,f(x)必有零点 |
分析 根据函数的单调性以及a的范围分别对各个选项进行判断即可.
解答 解:(1)a=2时,f(x)=lnx+$\frac{1}{2}$x2-2x+1,
f′(x)=$\frac{{(x-1)}^{2}}{x}$≥0,f(x)递增,无极值点,
故A错误;
(2)f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$+x-a≥2-a,
故-2<a<2时,f′(x)>0,
f(x)在(0,+∞)递增,函数无极值,
故B正确;
(3)a>2时,f′(x)=$\frac{{x}^{2}-ax+1}{x}$,
令g(x)=x2-ax+1,△=a2-4>0,
x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$>0,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$,
故f(x)在(0,$\frac{a-\sqrt{{a}^{2}-4}}{2}$)递增,在( $\frac{a-\sqrt{{a}^{2}-4}}{2}$,$\frac{a+\sqrt{{a}^{2}-4}}{2}$)递减,在( $\frac{a+\sqrt{{a}^{2}-4}}{2}$,+∞)递增;
故f(x)的极小值是f( $\frac{a+\sqrt{{a}^{2}-4}}{2}$)=ln $\frac{a+\sqrt{{a}^{2}-4}}{2}$-$\frac{{a}^{2}}{4}$-$\frac{a\sqrt{{a}^{2}-4}}{4}$+$\frac{1}{2}$<lna-$\frac{{a}^{2}}{2}$+$\frac{1}{2}$,
令h(a)=lna-$\frac{{a}^{2}}{2}$+$\frac{1}{2}$,(a>2),h′(a)=$\frac{1}{a}$-a<0,
故h(a)在(2,+∞)递减,h(a)<h(2)=ln2-$\frac{3}{2}$<0,
故a>2时,f(x)的极小值小于0,
故C正确;
(4)x→0时,f(x)→-∞,
x→+∞时,f(x)→+∞,
显然f(x)有零点,
故D正确;
故选:A.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
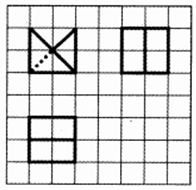 如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )
如图所示,网格纸上小正方形的边长为$\frac{1}{2}$,粗实线及粗虚线画出的是某几何体的三视图,则两个这样的几何体拼接而成的几何体表面积最小值为( )| A. | 5+2$\sqrt{2}$ | B. | 6+2$\sqrt{2}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
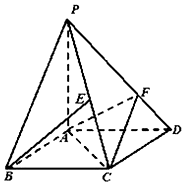 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上,且PF=2FD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com