练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
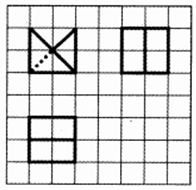
    13．如图所示，网格纸上小正方形的边长为$\frac{1}{2}$，粗实线及粗虚线画出的是某几何体的三视图，则两个这样的几何体拼接而成的几何体表面积最小值为（　　）
    A．5+2$\sqrt{2}$B．6+2$\sqrt{2}$C．5D．6

    分析 由三视图可知：该几何体为两个三棱柱组成的．则两个这样的几何体拼接而成的几何体表面积最小值时为正方体．

    解答 解：由三视图可知：该几何体为两个全等的直三棱柱组成的．
    则两个这样的几何体拼接而成的几何体表面积最小值时为正方体：
    因此最小表面积=12×6=6．
    故选：D．

    点评 本题考查了直三棱柱、正方体的三视图、面积计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．证明：若函数f（x）在区间[a，b]上是增函数，那么方程f（x）=0在区间[a，b]上至多只有一个实数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

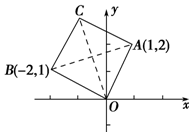    4．如图在复平面上，一个正方形的三个顶点对应的复数分别是1+2i，-2+i，0，那么这个正方形的第四个顶点对应的复数为（　　）
    A．3+iB．-1+3iC．1-3iD．3-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．某几何体的三视图如图所示，其正视图，侧视图，俯视图均为全等的正方形，则该几何体的体积为（　　）
    A．$\frac{4}{3}$B．$\frac{8}{3}$C．$\sqrt{6}$D．2$\sqrt{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．（文科）等差数列{an}的首项a1=3，a5=11，bn=an-12
    （1）求an和{ bn}的前n项和Sn；
    （2）若Tn=|b1|+|b2|+…+|bn|，求Tn；
    （3）设cn=$\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{cn}的前n项和Rn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．计算下列定积分．
    （1）$\int_0^1{（2x+3）dx}$；
    （2）$\int_e^{e^3}{\frac{1}{x}}dx$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

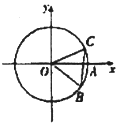    5．∠AOB如图，⊙O与x轴的正半轴交点为A，点B，C在⊙O上，且$B（\frac{3}{5}，-\frac{4}{5}）$，点C在第一象限，∠AOC=α，BC=1，则$cos（\frac{5π}{6}-α）$=（　　）
    A．$-\frac{4}{5}$B．$-\frac{3}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

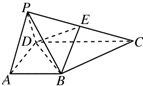    6．已知在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=90°，2AB=2AD=CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC的中点．
    （1）求证：BE⊥平面PCD；
    （2）在PB上是否存在一点F，使AF∥平面BDE？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数$f（x）=lnx+\frac{1}{2}{x^2}-ax+1$，下列结论中错误的是（　　）
    A．当a=2时，x=1是f（x）的一个极值点B．当-2＜a＜2时，函数f（x）无极值
    C．当a＞2时，f（x）的极小值小于0D．?a∈R，f（x）必有零点

    查看答案和解析>>

    同步练习册答案