
分析 (1)由抛物线方程求出抛物线焦点坐标,得到椭圆的长半轴长,结合离心率求得c,再由隐含条件求得b,则椭圆方程可求;
(2)联立直线方程和椭圆方程,利用根与系数的关系求出A、B的横坐标的和与积,结合已知可得m与k的关系,求出弦长,再由点到直线的距离公式求出O到直线AB的距离,代入三角形面积公式即可证得△AOB的面积为定值.
解答 (1)解:抛物线y2=-8x的焦点为(-2,0),故a=2,又$\frac{c}{a}=\frac{1}{2}$,故c=1,$b=\sqrt{3}$.
∴椭圆Ω的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)证明:设A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3+4k2)x2+8mkx+4m2-12=0.
∵△=(8mk)2-4(3+4k2)(4m2-12)=48(3+4k2-m2)>0,
∴3+4k2-m2>0,∴${x_1}+{x_2}=\frac{-8mk}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4({m^2}-3)}}{{3+4{k^2}}}$,
∴${y_1}{y_2}=(k{x_1}+m)(k{x_2}+m)={k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}=\frac{{3{m^2}-12{k^2}}}{{3+4{k^2}}}$.
由3x1x2+4y1y2=0,得$3•\frac{{4({m^2}-3)}}{{3+4{k^2}}}+4•\frac{{3{m^2}-12{k^2}}}{{3+4{k^2}}}=0$,
∴2m2=3+4k2.
∵$|AB|=\sqrt{1+{k^2}}|{x_1}-{x_2}|=\sqrt{1+{k^2}}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{1+{k^2}}•\sqrt{\frac{{48(3+4{k^2}-{m^2})}}{{{{(3+4{k^2})}^2}}}}$
=$\sqrt{1+{k^2}}•\sqrt{\frac{{48(2{m^2}-{m^2})}}{{{{(2{m^2})}^2}}}}=\sqrt{(1+{k^2})}•\sqrt{\frac{12}{m^2}}$,
又点O到直AB线的距离$d=\frac{|m|}{{\sqrt{1+{k^2}}}}=\frac{{\sqrt{m^2}}}{{\sqrt{1+{k^2}}}}$,
∴${S_{△AOB}}=\frac{1}{2}|AB|•d=\frac{1}{2}•\sqrt{1+{k^2}}•\sqrt{\frac{12}{m^2}}•\frac{{\sqrt{m^2}}}{{\sqrt{1+{k^2}}}}=\sqrt{3}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查弦长公式的应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
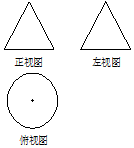 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a=2时,x=1是f(x)的一个极值点 | B. | 当-2<a<2时,函数f(x)无极值 | ||
| C. | 当a>2时,f(x)的极小值小于0 | D. | ?a∈R,f(x)必有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
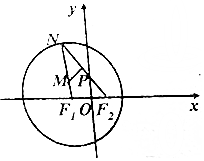 已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.
已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com