
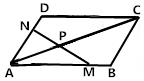
 ��ͼ����?ABCD�У�M��N�ֱ�ΪAB��AD�ϵĵ㣬��$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$������AC��MN����P�㣬��$\overrightarrow{AP}$=��$\overrightarrow{AC}$����˵�ֵΪ��������
��ͼ����?ABCD�У�M��N�ֱ�ΪAB��AD�ϵĵ㣬��$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$������AC��MN����P�㣬��$\overrightarrow{AP}$=��$\overrightarrow{AC}$����˵�ֵΪ��������| A�� | $\frac{3}{5}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{6}{13}$ | D�� | $\frac{6}{17}$ |
���� $\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$����$\overrightarrow{AP}$=��$\overrightarrow{AC}$=�ˣ�$\overrightarrow{AB}+\overrightarrow{AD}��$=$�ˣ�\frac{3}{2}\overrightarrow{AN}+\frac{4}{3}\overrightarrow{AM}��=\frac{3}{2}��\overrightarrow{AN}+\frac{4}{3}��\overrightarrow{AM}$������M��N��P���ߣ�$\frac{3}{2}��+\frac{4}{3}��=1$��������æˣ�
��� �⣺�� $\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$����$\overrightarrow{AP}$=��$\overrightarrow{AC}$=�ˣ�$\overrightarrow{AB}+\overrightarrow{AD}��$
$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$����$\overrightarrow{AP}$=��$\overrightarrow{AC}$=�ˣ�$\overrightarrow{AB}+\overrightarrow{AD}��$
=$�ˣ�\frac{3}{2}\overrightarrow{AN}+\frac{4}{3}\overrightarrow{AM}��=\frac{3}{2}��\overrightarrow{AN}+\frac{4}{3}��\overrightarrow{AM}$��
������M��N��P���ߣ���$\frac{3}{2}��+\frac{4}{3}��=1$�����=$\frac{6}{17}$��
��ѡ��D��
���� ���⿼����ƽ���������������㣬�����㹲�ߵij�Ҫ�����������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��p��qΪ�����⣬��p��q��Ϊ������ | |
| B�� | ���⡰��x2=1����x=1��Ϊ������ | |
| C�� | ���⡰��x=y����sinx=siny�����������Ϊ������ | |
| D�� | ���⡰����һ��ʵ��x��ʹ����ʽx2-3x+6��0������Ϊ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 0 | C�� | 3 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{��}{9}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��$\frac{5��}{6}$�� | B�� | ��2��$\frac{2��}{3}$�� | C�� | ��2��$\frac{5��}{3}$�� | D�� | ��2��$\frac{11��}{6}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
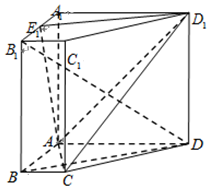 ��ͼ����������ABCD-A1B1C1D1�У�����AA1�͵���ABCD������ABCD��ֱ�����Σ�AD��BC����BAD=90�㣬AD=AA1=3��BC=1��AB=$\sqrt{3}$��E1ΪA1B1�е㣮
��ͼ����������ABCD-A1B1C1D1�У�����AA1�͵���ABCD������ABCD��ֱ�����Σ�AD��BC����BAD=90�㣬AD=AA1=3��BC=1��AB=$\sqrt{3}$��E1ΪA1B1�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | $\frac{32}{3}��$ | C�� | $\frac{16}{3}��$ | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com