
分析 (1)假设函数 $f(x)=\frac{1}{x}$有“可增点”,则$\frac{1}{{{x_0}+1}}≥\frac{1}{x_0}+1$,⇒$\frac{{{x}_{0}}^{2}+{x}_{0}+1}{{x}_{0}({x}_{0}+1)}≤0$即x02(x0+1)<0,解出x0即可,
(2)若$f(x)=lg({\frac{a}{{{x^2}+1}}})$ 在(0,+∞)上存在可增点,即有$lg\frac{a}{{{{({{x_0}+1})}^2}+1}}≥lg({\frac{a}{{{x_0}^2+1}}})+lg\frac{a}{2}$成立,即不等式$({a-2}){x_0}^2+2a{x_0}-2+2a≤0$在(0,+∞)上有解,记$g(x)=({a-2}){x_0}^2+2a{x_0}-2+2a$,分a=2,0<a<2,a>2讨论即可.
解答 解:(1)假设函数 $f(x)=\frac{1}{x}$有“可增点”,则$\frac{1}{{{x_0}+1}}≥\frac{1}{x_0}+1$⇒$\frac{{{x}_{0}}^{2}+{x}_{0}+1}{{x}_{0}({x}_{0}+1)}≤0$
即x02(x0+1)<0,∴-1<x0<0,
所以函数$f(x)=\frac{1}{x}$ 存在可增点,∴-1<x0<0.
(2)若$f(x)=lg({\frac{a}{{{x^2}+1}}})$ 在(0,+∞)上存在可增点,即有$lg\frac{a}{{{{({{x_0}+1})}^2}+1}}≥lg({\frac{a}{{{x_0}^2+1}}})+lg\frac{a}{2}$成立,
即$\frac{a}{{{{({{x_0}^2+1})}^2}+1}}≥\frac{a}{{{x_0}^2+1}}•\frac{a}{2}$,且a>0,
依题意不等式$({a-2}){x_0}^2+2a{x_0}-2+2a≤0$在(0,+∞)上有解,
记$g(x)=({a-2}){x_0}^2+2a{x_0}-2+2a$,
当a=2时,${x_0}≤-\frac{1}{2}$,不符合条件;
当0<a<2时,a-2<0,函数g(x)开口向下,符合条件;
当a>2时,函数g(x)的对称轴$x=\frac{a}{2-a}<0$,且g(0)=2a-2>0,所以在(0,+∞)上g(x)>0,不符合.
综上可得0<a<2.
点评 本题考查了学生的分析能力及分类讨论的思想应用,同时考查了不等式及对数函数应用,属于基础题.


科目:高中数学 来源: 题型:选择题
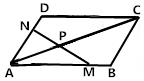 如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{13}$ | D. | $\frac{6}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x$\sqrt{ax}$ | B. | x$\sqrt{-ax}$ | C. | -x$\sqrt{-ax}$ | D. | -x$\sqrt{ax}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=2 | B. | (x-1)2+(y+1)2=5 | C. | (x+1)2+(y-1)2=1 | D. | (x+1)2+(y+2)2=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com