Question

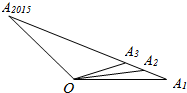
11．如图，O为直线A₁A₂₀₁₅外一点，若A₁，A₂，A₃，A₄，A₅…A₂₀₁₅中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（　　）

• A． 2014（$\overrightarrow{a}+\overrightarrow{b}$）
• B． 2015（$\overrightarrow{a}+\overrightarrow{b}$）
• C． $\frac{2014}{2}$（$\overrightarrow{a}+\overrightarrow{b}$）
• D． $\frac{2015}{2}$（$\overrightarrow{a}+\overrightarrow{b}$）

Answer 1

分析 可设线段A₁A₂₀₁₅的中点为P，根据题意便有$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2015}}=2\overrightarrow{OP}$，$\overrightarrow{O{A}_{2}}+\overrightarrow{O{A}_{2014}}=2\overrightarrow{OP}$，…，$\overrightarrow{O{A}_{1007}}+\overrightarrow{O{A}_{1009}}=2\overrightarrow{OP}$，$\overrightarrow{O{A}_{1008}}=\overrightarrow{OP}$，从而可以用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$．

解答 解：设线段A₁A₂₀₁₅的中点为P，则$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2015}}=2\overrightarrow{OP}$，$\overrightarrow{O{A}_{2}}+\overrightarrow{O{A}_{2014}}=2\overrightarrow{OP}$，…，$\overrightarrow{O{A}_{1007}}+\overrightarrow{O{A}_{1009}}=2\overrightarrow{OP}$，$\overrightarrow{O{A}_{1008}}=\overrightarrow{OP}$；
∴$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}=1007$$（\overrightarrow{a}+\overrightarrow{b}）$$+\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）$=$\frac{2015}{2}（\overrightarrow{a}+\overrightarrow{b}）$．
故选D．

点评 考查向量加法的平行四边形法则，向量数乘的几何意义及其运算．