
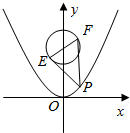
分析 设F(cosθ,4+sinθ),可得E(-cosθ,4-sinθ).设P$(t,\frac{1}{2}{t}^{2})$,可得$\overrightarrow{PE}•\overrightarrow{PF}$=$\frac{1}{4}({t}^{2}-6)^{2}+6$,利用二次函数的单调性即可得出.
解答 解:设F(cosθ,4+sinθ),∵EF是曲线C1的任意一条直径,则E(-cosθ,4-sinθ).
设P$(t,\frac{1}{2}{t}^{2})$,
则$\overrightarrow{PE}•\overrightarrow{PF}$=(-cosθ-t,4-sinθ-$\frac{1}{2}{t}^{2}$)•(cosθ-t,4+sinθ-$\frac{1}{2}{t}^{2}$)=t2-cos2θ+$(4-\frac{1}{2}{t}^{2})^{2}-si{n}^{2}θ$
=$\frac{1}{4}{t}^{4}-3{t}^{2}+15$
=$\frac{1}{4}({t}^{2}-6)^{2}+6$≥6,
当$t=±\sqrt{6}$时,取等号.
∴$\overrightarrow{PE}•\overrightarrow{PF}$的最小值为6.
故答案为:6.
点评 本题考查了向量数量积的坐标运算、圆与抛物线的参数方程,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.
如图,在平行四边形ABCD中,∠BAD=120°,AB=2,AD=1,若$\overrightarrow{DE}=t\overrightarrow{DC}$,AE⊥BD,则实数t的值为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
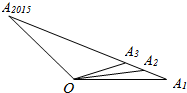 如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )| A. | 2014($\overrightarrow{a}+\overrightarrow{b}$) | B. | 2015($\overrightarrow{a}+\overrightarrow{b}$) | C. | $\frac{2014}{2}$($\overrightarrow{a}+\overrightarrow{b}$) | D. | $\frac{2015}{2}$($\overrightarrow{a}+\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
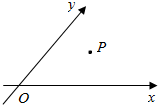 如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).
如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com