
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 求函数的导数,先求出和y=x+1+b平行的切线方程,建立a,b的关系,作出不等式组对应的平面区域,求出对应的面积,利用几何概型的概率公式进行求解即可.
解答  解:y=ex+$\sqrt{a}$的导数f′(x)=ex,和y=x+1+b平行的切线斜率k=f′(x)=1,
解:y=ex+$\sqrt{a}$的导数f′(x)=ex,和y=x+1+b平行的切线斜率k=f′(x)=1,
即由ex=1,得x=0,此时f(0)=1+$\sqrt{a}$,即切点坐标为(0,1+$\sqrt{a}$),
对应的切线方程为y-1-$\sqrt{a}$=x,即y=x+1+$\sqrt{a}$,
若曲线C1与C2有交点,则1+b≥1+$\sqrt{a}$,即b≥$\sqrt{a}$,
作出对应的不等式如图:
则正方体OABC的面积S=1,阴影部分的面积S=1-∫${\;}_{0}^{1}$$\sqrt{a}$da=1-$\frac{2}{3}$a${\;}^{\frac{3}{2}}$|${\;}_{0}^{1}$=1-$\frac{2}{3}$=$\frac{1}{3}$,
则曲线C1与C2有交点的概率P=$\frac{\frac{1}{3}}{1}=\frac{1}{3}$,
故选:D.
点评 本题主要考查几何概型的概率的计算,涉及导数的几何意义,利用积分求面积,综合性较强,有一定的难度.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
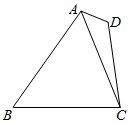 如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.
如图,在四边形ABCD中,△ACB与∠D互补,cos∠ACB=$\frac{1}{3}$,AC=BC=2$\sqrt{3}$,AB=4AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(x+$\frac{π}{2}$)+1 | B. | y=sin(x-$\frac{π}{2}$)+1 | C. | y=sin(x+$\frac{π}{4}$)+1 | D. | y=sin(x-$\frac{π}{4}$)+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}⊥\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$| | C. | θ∈(0,$\frac{π}{2}$) | D. | $θ∈(\frac{π}{2},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
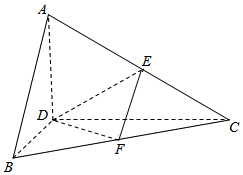 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b∈R,且a+b>4,则a,b至少有一个大于2 | |
| B. | “?x0∈R,${2^{x_0}}=1$”的否定是“?x∈R,2x≠1” | |
| C. | a>1,b>1是ab>1的必要条件 | |
| D. | △ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com