Question

10．已知x，y满足$\left\{\begin{array}{l}{x+3y≤5π}\\{x-y≥0}\\{y≥0}\end{array}\right.$，则sin（$\frac{x}{4}$-$\frac{y}{2}$）的取值范围是[-sin$\frac{5π}{16}$，1]．

Answer 1

分析 利用线性规划求出$\frac{x}{4}-\frac{y}{2}$的范围，根据正弦函数的单调性得出sin（$\frac{x}{4}$-$\frac{y}{2}$）的取值范围．

解答 解：作出约束条件表示的可行域如图：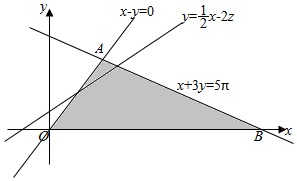

令z=$\frac{x}{4}-\frac{y}{2}$得y=$\frac{x}{2}$-2z，
∴当直线y=$\frac{x}{2}$-2z经过点A时截距最大，即z最小，
当直线y=$\frac{x}{2}$-2z经过点B时截距最小，即z最大．
解方程组$\left\{\begin{array}{l}{x-y=0}\\{x+3y=5π}\end{array}\right.$得A（$\frac{5π}{4}$，$\frac{5π}{4}$），
∴z的最小值为$\frac{5π}{16}-\frac{5π}{8}$=-$\frac{5π}{16}$，
解方程组$\left\{\begin{array}{l}{y=0}\\{x+3y=5π}\end{array}\right.$得B（5π，0）．
∴z的最大值为$\frac{5π}{4}$．
∴-$\frac{5π}{16}$≤$\frac{x}{4}-\frac{y}{2}$≤$\frac{5π}{4}$．
∴当$\frac{x}{4}-\frac{y}{2}$=$\frac{π}{2}$时，sin（$\frac{x}{4}-\frac{y}{2}$）取得最大值1．
当$\frac{x}{4}-\frac{y}{2}$=-$\frac{5π}{16}$时，sin（$\frac{x}{4}-\frac{y}{2}$）取得最小值sin（-$\frac{5π}{16}$）=-sin$\frac{5π}{16}$，
故答案为[-sin$\frac{5π}{16}$，1]．

点评 本题考查了简单的线性规划，正弦函数的图形与性质，属于中档题．