
分析 由“函数y=loga(x+1)在区间(0,+∞)内单调递减”,可知p:0<a<1.由“曲线y=x2+(2a-3)x+1与x轴交于不同的两点”,可得△>0.因为“p∨q”为真命题,“p∧q”为假命题,所以p与q恰好一真一假,即可得出.
解答 解:由“函数y=loga(x+1)在区间(0,+∞)内单调递减”,
可知p:0<a<1,
由“曲线y=x2+(2a-3)x+1与x轴交于不同的两点”,∴△=(2a-3)2-4>0,a>0,a≠1.
可知$q:a>\frac{5}{2}$或$0<a<\frac{1}{2}$,
因为“p∨q”为真命题,“p∧q”为假命题,
所以p与q恰好一真一假,
当p真,q假时,$a∈({0,1})∩[{\frac{1}{2},\frac{5}{2}}]$,即$a∈[{\frac{1}{2},1})$.
当p假,q真时,$a∈({1,+∞})∩({({0,\frac{1}{2}})∪({\frac{5}{2},+∞})})$,即$a∈({\frac{5}{2},+∞})$.
综上可知,a的取值范围为:$[{\frac{1}{2},1})∪({\frac{5}{2},+∞})$.
点评 本题考查了函数的性质、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<2} | B. | {x|-2≤x≤1} | C. | {-2,-1,0,1,2} | D. | {-2,-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{7}$ | B. | 7 | C. | $\frac{1}{7}$ | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
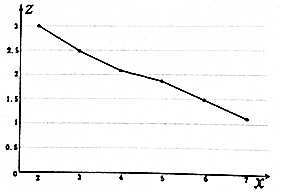
| 使用年数x | 2 | 3 | 4 | 5 | 6 | 7 |
| 售价y | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| z=lny | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com