
已知:a>0,b>0,a+b=1.求证: ≤2.
≤2.
科目:高中数学 来源: 题型:
从参加某次高三数学摸底考试的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
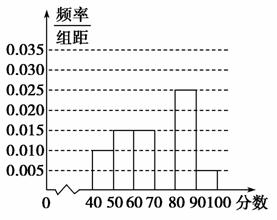
(1)补全这个频率分布直方图,并估计本次考试的平均分;
(2)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总得分,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
A.(7,5) B.(5,7)
C.(2,10) D.(10,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)定义如表,数列{xn}满足x1=5,xn+1=f(xn),则x2014的值为________.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 4 | 5 | 1 | 2 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“⊳”.定义如下:对于任意两个复数z1=a1+b1i,z2=a2+b2i(a1、b1、a2、b2∈R,i为虚数单位),当且仅当“a1>a2”或“a1=a2且b1>b2时,z1⊳z2”.下列命题为假命题的是( )
A.1⊳i⊳0
B.若z1⊳z2,z2⊳z3,则z1⊳z3
C.若z1⊳z2,则对于任意z∈C,z1+z⊳z2+z
D.对于复数z⊳0,若z1 ⊳z2,则z·z1⊳z·z2
查看答案和解析>>
科目:高中数学 来源: 题型:
观察①sin210°+cos240°+sin10°cos40°=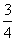 ;
;
②sin26°+cos236°+sin6°cos36°=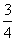 .
.
由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com