
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“⊳”.定义如下:对于任意两个复数z1=a1+b1i,z2=a2+b2i(a1、b1、a2、b2∈R,i为虚数单位),当且仅当“a1>a2”或“a1=a2且b1>b2时,z1⊳z2”.下列命题为假命题的是( )
A.1⊳i⊳0
B.若z1⊳z2,z2⊳z3,则z1⊳z3
C.若z1⊳z2,则对于任意z∈C,z1+z⊳z2+z
D.对于复数z⊳0,若z1 ⊳z2,则z·z1⊳z·z2
D
[解析] 对于A,注意到1=1+0×i,i=0+1×i,0=0+0×i,1>0,则1⊳i,0=0且1>0,则i⊳0,因此有1⊳i⊳0,A正确.对于B,由z1⊳z2得“a1>a2”或“a1=a2且b1>b2”;由z2⊳z3得“a2>a3”或“a2=a3且b2>b3”,于是有“a1>a3”或“a1=a3且b1>b3”,即有z1⊳z3,选项B正确.对于C,设z=a+bi,由z1⊳z2得“a1>a2”或“a1=a2且b1>b2”,所以“a1+a>a2+a”或“a1+a=a2+a且b1+b>b2+b”,即有z1+z⊳z2+z,因此选项C正确.对于D,取z=1-2i⊳0,z1=3,z2=3i,此时z·z1=3-6i,z·z2=6+3i,z·z2⊳z·z1,因此选项D不正确.综上所述,选D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
袋中有5个小球(3白2黑),现从袋中每次取一个球,不放回地抽取两次,则在第一次取到白球的条件下,第二次取到白球的概率是( )
A.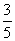 B.
B.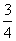
C.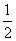 D.
D.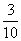
查看答案和解析>>
科目:高中数学 来源: 题型:
若定义在区间D上的函数f(x),对于D上的任意n个值x1、x2、…、xn,总满足f(x1)+f(x2)+…+f(xn)≥nf ,则称f(x)为D上的凹函数,现已知f(x)=tanx在
,则称f(x)为D上的凹函数,现已知f(x)=tanx在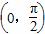 上是凹函数,则在锐角三角形ABC中,tanA+tanB+tanC的最小值是( )
上是凹函数,则在锐角三角形ABC中,tanA+tanB+tanC的最小值是( )
A.3 B.
C.3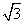 D.
D.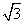
查看答案和解析>>
科目:高中数学 来源: 题型:
经过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2.类比上述性质,可以得到椭圆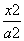 +
+ =1类似的性质为:经过椭圆
=1类似的性质为:经过椭圆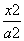 +
+ =1上一点P(x0,y0)的切线方程为________.
=1上一点P(x0,y0)的切线方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线C:y2=2x(y≥0),A1(x1,y1),A2(x2,y2),…,An(xn,yn),…是曲线C上的点,且满足0<x1<x2<…<xn<…,一列点Bi(ai,0)(i=1,2,…)在x轴上,且△Bi-1AiBi(B0是坐标原点)是以Ai为直角顶点的等腰直角三角形.
(1)求A1,B1的坐标;
(2)求数列{yn}的通项公式;
(3)令bi=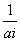 ,ci=
,ci=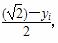 ,是否存在正整数N,当n≥N时,都有
,是否存在正整数N,当n≥N时,都有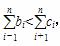 ,若存在,求出N的最小值并证明;若不存在,说明理由.
,若存在,求出N的最小值并证明;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com