经过圆x2+y2＝r2上一点M(x0.y0)的切线方程为x0x+y0y＝r2.类比上述性质.可以得到椭圆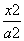+＝1类似的性质为:经过椭圆+＝1上一点P(x0.y0)的切线方程为．题目和参考答案——青夏教育精英家教网—

经过圆x²＋y²＝r²上一点M(x₀，y₀)的切线方程为x₀x＋y₀y＝r².类比上述性质，可以得到椭圆＋＝1类似的性质为：经过椭圆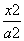＋＝1上一点P(x₀，y₀)的切线方程为________．

＝1

[解析]　过圆上一点M(x₀，y₀)的切线方程是把圆的方程中的x²、y²中的一个x和一个y分别用x₀、y₀代替，圆和椭圆都是封闭曲线，类比圆上一点的切线方程可以得到，过椭圆上一点P(x₀，y₀)的切线方程也是把椭圆方程中的x²、y²中的一个x和一个y分别用x₀、y₀代替，即得到切线方程为＋＝1.

例如过椭圆＋y²＝1上一点(1，)的切线方程为＋y＝1，即x＋2y－4＝0.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

一台机器生产某种产品，如果生产一件甲等品可获利50元，生产一件乙等品可获利30元，生产一件次品，要赔20元，已知这台机器生产甲等品、乙等品和次品的概率分别为0.6、0.3和0.1，则这台机器每生产一件产品，平均预期可获利(　　)

A．39元 B．37元

C．20元 D.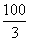元

查看答案和解析>>

科目：高中数学 来源： 题型：

设i是虚数单位，复数为纯虚数，则实数a为(　　)

A．2 B．－2

C．－ D.

查看答案和解析>>

科目：高中数学 来源： 题型：

已知x∈(0，＋∞)，观察下列各式：x＋≥2，x＋＝＋＋≥3，x＋＝＋＋＋≥4，…，类比得x＋≥n＋1(n∈N^*)，则a＝________.

查看答案和解析>>

科目：高中数学 来源： 题型：

在实数集R中，我们定义的大小关系“>”为全体实数排了一个“序”，类似地，我们在复数集C上也可以定义一个称为“序”的关系，记为“⊳”．定义如下：对于任意两个复数z₁＝a₁＋b₁i，z₂＝a₂＋b₂i(a₁、b₁、a₂、b₂∈R，i为虚数单位)，当且仅当“a₁>a₂”或“a₁＝a₂且b₁>b₂时，z₁⊳z₂”．下列命题为假命题的是(　　)