
计划在某水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5 000万元;若某台发电机未运行,则该台年亏损800万元.欲使水电站年总利润的均值达到最大,应安装发电机多少台.
解 (1)依题意,p1=P(40<X<80)=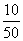 =0.2,
=0.2,
p2=P(80≤X≤120)=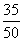 =0.7,
=0.7,
p3=P(X>120)=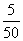 =0.1.
=0.1.
由二项分布,在未来4年中至多有1年的年入流量超过120的概率为】
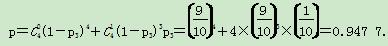 (2)记水电站年总利润为Y(单位:万元).
(2)记水电站年总利润为Y(单位:万元).
①安装1台发电机的情形.
由于水库年入流量总大于40,故1台发电机运行的概率为1,对应的年利润Y=5 000,E(Y)=5 000×1=5 000.
②安装2台发电机的情形.
依题意,当40<X<80时,1台发电机运行,此时Y=5 000-800=4 200,因此P(Y=4 200)=P(40<X<80)=p1=0.2;
当X≥80时,2台发电机运行,此时Y=5 000×2=10 000,因此P(Y=10 000)=P(X≥80)=p2+p3=0.8;由此得Y的分布列如下:
| Y | 4 200 | 10 000 |
| P | 0.2 | 0.8 |


科目:高中数学 来源: 题型:
在如图11所示的空间直角坐标系O xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )
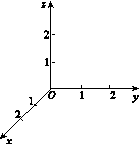
图11
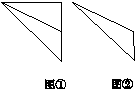
A.①和② B.①和③ C.③和② D.④和②
查看答案和解析>>
科目:高中数学 来源: 题型:
四面体ABCD及其三视图如图14所示,过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
(1)证明:四边形EFGH是矩形;
(2)求直线AB与平面EFGH夹角θ的正弦值.
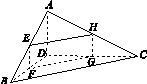
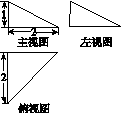
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
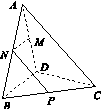
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
一名同学先后投掷一枚骰子两次,第一次向上的点数记为x,第二次向上的点数记为y,在直角坐标系xOy中,以(x,y)为坐标的点落在直线2x+y=8上的概率为( )
A.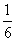 B.
B.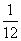
C.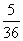 D.
D.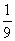
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com