
分析 根据向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标表示,求出$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值,由此列出方程求出x的值.
解答 解:向量$\overrightarrow{a}$=(x,4,5),$\overrightarrow{b}$=(1,-2,2),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=x-2×4+2×5=x+2,
|$\overrightarrow{a}$|=$\sqrt{{x}^{2}{+4}^{2}{+5}^{2}}$=$\sqrt{{x}^{2}+41}$,
|$\overrightarrow{b}$|=$\sqrt{{1}^{2}{+(-2)}^{2}{+2}^{2}}$=3;
又$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值为:
cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{x+2}{\sqrt{{x}^{2}+41}×3}$=$\frac{\sqrt{2}}{6}$,
整理得x2+8x-33=0,
解得x=-11(不合题意,舍去)或x=3;
∴x的值为3.
故答案为:3.
点评 本题考查了空间向量的数量积的应用问题,也考查了两向量夹角余弦的应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{4}{5}$,$\frac{3}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$),($\frac{3}{5}$,$\frac{4}{5}$) | D. | ($±\frac{3}{5}$,$±\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:选择题
设函数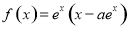 (其中
(其中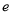 为自然对数的底数)恰有两个极值点
为自然对数的底数)恰有两个极值点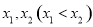 ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.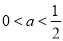 B.
B.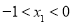
C.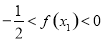 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com