
分析 根据幂函数y=${x}^{\frac{2}{3}}$的图象与性质判断${2}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$,再根据指数函数的图象与性质判断${(\frac{4}{3})}^{\frac{2}{3}}$>1,${(\frac{3}{4})}^{\frac{1}{3}}$<1;
由此比较题目中各数的大小.
解答 解:∵幂函数y=${x}^{\frac{2}{3}}$在(0,+∞)上是单调增函数,且2>$\frac{4}{3}$,
∴${2}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$;
又根据指数函数的图象与性质得${(\frac{4}{3})}^{\frac{2}{3}}$>1,${(\frac{3}{4})}^{\frac{1}{3}}$<1;
∴2${\;}^{\frac{2}{3}}$>${(\frac{4}{3})}^{\frac{2}{3}}$>1>($\frac{3}{4}$)${\;}^{\frac{1}{3}}$.
点评 本题考查了利用函数的图象与性质比较大小的应用问题,是基础题目.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数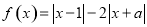 .
.
(1)当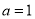 时,求不等式
时,求不等式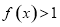 的解集;
的解集;
(2)若不等式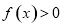 ,在
,在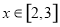 上恒成立,求
上恒成立,求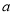 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届浙江嘉兴市高三上学期基础测试数学试卷(解析版) 题型:选择题
已知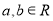 ,则“
,则“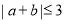 ”是“
”是“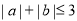 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com