
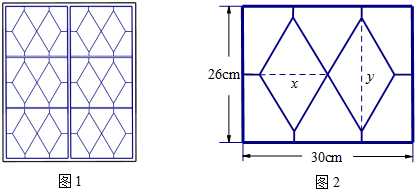
分析 (1)分别求出水平方向每根支条长、竖直方向每根支条长、菱形的边长,即可用x,y表示L;
(2)$L=82+4\sqrt{{x^2}+{{(\frac{260}{x})}^2}}-2(x+\frac{260}{x})$.换元,求导确定函数的单调性,即可得出结论.
解答 解:(1)由题意,水平方向每根支条长为$m=\frac{30-2x}{2}=15-x$ cm,竖直方向每根支条长为$n=\frac{26-y}{2}=13-\frac{y}{2}$ cm,菱形的边长为$\sqrt{{{(\frac{x}{2})}^2}+{{(\frac{y}{2})}^2}}=\frac{{\sqrt{{x^2}+{y^2}}}}{2}$ cm.
从而,所需木料的长度之和L=$2(15-x)+4(13-\frac{y}{2})+8×\frac{{\sqrt{{x^2}+{y^2}}}}{2}$=$82+4\sqrt{{x^2}+{y^2}}-2(x+y)$ cm.
(2)由题意,$\frac{1}{2}xy=13$,即$y=\frac{260}{x}$,
又由$\left\{{\begin{array}{l}{15-x≥2}\\{13-\frac{y}{2}≥2}\end{array}}\right.$ 可得$\frac{130}{11}≤x≤13$.所以$L=82+4\sqrt{{x^2}+{{(\frac{260}{x})}^2}}-2(x+\frac{260}{x})$.
令$t=x+\frac{260}{x}$,其导函数$1-\frac{260}{x^2}<0$ 在$\frac{130}{11}≤x≤13$ 上恒成立,
故$t=x+\frac{260}{x}$ 在$[\frac{130}{11},13]$ 上单调递减,
所以可得$t∈[33,\frac{372}{11}]$.
则$L=82+2[2\sqrt{{{(x+\frac{260}{x})}^2}-520}-(x+\frac{260}{x})]$=$82+2[\sqrt{{t^2}-520}+\sqrt{{t^2}-520}-t]$
=$82+2[\sqrt{{t^2}-520}+\frac{-520}{{\sqrt{{t^2}-520}+t}}]$.
因为函数$y=\sqrt{{t^2}-520}$ 和$y=\frac{-520}{{\sqrt{{t^2}-520}+t}}$ 在$t∈[33,\frac{372}{11}]$ 上均为增函数,
所以$L=82+2[\sqrt{{t^2}-520}+\frac{-520}{{\sqrt{{t^2}-520}+t}}]$ 在$t∈[33,\frac{372}{11}]$ 上为增函数,
故当t=33,即x=130,y=20 时L有最小值$16+4\sqrt{569}$.
答:做这样一个窗芯至少需要$16+4\sqrt{569}$ cm长的条形木料.
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,确定函数关系是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
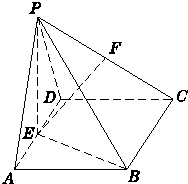 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com