
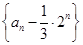 是等比数列;
是等比数列;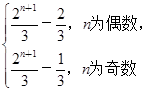 (3)t<1
(3)t<1 ·2n+1=-
·2n+1=-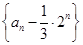 ,
,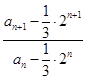 =-1,∴
=-1,∴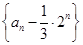 是等比数列,
是等比数列,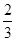 =
= ,q=-1,∴an=
,q=-1,∴an= [2n-(-1)n].
[2n-(-1)n]. (2+22+…+2n)-
(2+22+…+2n)- [(-1)+(-1)2+…+(-1)n]=
[(-1)+(-1)2+…+(-1)n]=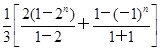
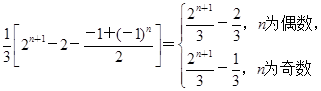
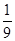 [2n-(-1)n][2n+1-(-1)n+1]=
[2n-(-1)n][2n+1-(-1)n+1]=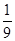 [22n+1-(-2)n-1],∴bn-t·Sn>0,
[22n+1-(-2)n-1],∴bn-t·Sn>0,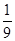 [22n+1-(-2)n-1]-t·
[22n+1-(-2)n-1]-t·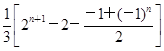 >0,∴当n为奇数时,
>0,∴当n为奇数时,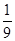 (22n+1+2n-1)-
(22n+1+2n-1)-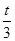 (2n+1-1)>0,∴t<
(2n+1-1)>0,∴t< (2n+1)对任意的n为奇数都成立,∴t<1.
(2n+1)对任意的n为奇数都成立,∴t<1.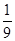 (22n+1-2n-1)-
(22n+1-2n-1)-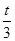 (2n+1-2)>0,
(2n+1-2)>0,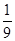 (22n+1-2n-1)-
(22n+1-2n-1)-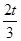 (2n-1)>0,
(2n-1)>0,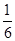 (2n+1+1)对任意的n为偶数都成立,∴t<
(2n+1+1)对任意的n为偶数都成立,∴t<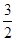 .
.

科目:高中数学 来源:不详 题型:解答题
 +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多 a万元.
a万元.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
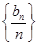 为等比数列,并求数列{bn}的通项公式.
为等比数列,并求数列{bn}的通项公式.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
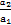 ,
,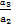 ,…,
,…, ,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )| A.25050 | B.24950 | C.2100 | D.299 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
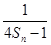 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
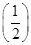 =________.
=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com