
分析 先由条件,得到loga$\frac{2}{a}$>loga$\frac{3}{a}$,从而求出a的取值范围,利用对数函数的单调性与特殊点化简不等式f(1-$\frac{1}{x}$)>1为整式不等式即可求解.
解答 解:∵满足f($\frac{2}{a}$)>f($\frac{3}{a}$),
∴loga$\frac{2}{a}$>loga$\frac{3}{a}$,
∴loga2>loga3,
∴0<a<1,
∵f(1-$\frac{1}{x}$)>1,
∴loga(1-$\frac{1}{x}$)>logaa,
∴0<1-$\frac{1}{x}$<a,
解得x∈(1,$\frac{1}{1-a}$).
故答案为:(1,$\frac{1}{1-a}$).
点评 本小题主要考查函数单调性的应用、对数函数的单调性与特殊点、不等式的解法等基础知识,考查运算求解能力与转化思想.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定构成三角形 | B. | 一定共线 | C. | 不一定共线 | D. | 与A,E共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{\sqrt{3}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
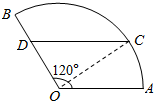 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )| A. | $50\sqrt{5}$ | B. | $50\sqrt{7}$ | C. | $50\sqrt{11}$ | D. | $50\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com