Question

4．将直角边长为1的等腰直角△ABC沿x轴正方向滚动，某时刻A与坐标原点重合（如图），设顶点A（x，y）的轨迹方程是y=f（x），关于函数y=f（x）有下列说法：
①f（x）的值域为[0，$\sqrt{2}$]；
②f（x）是周期函数且周期为1+$\sqrt{2}$；
③f（x）的一个减区间是[$\sqrt{2}$，$\sqrt{2}$+2]；
④${∫}_{0}^{\sqrt{2}+1}$f（x）dx=$\frac{3π}{4}$+$\frac{1}{2}$；
⑤f（1）＜f（$\sqrt{2}$+1）＜f（100+51$\sqrt{2}$）．
其中正确命题的序号为①③④．

Answer 1

分析 根据题意找准动点的运动规律，能画出判断，注意特殊位置，特殊点的确定，据此判断各个答案正确与否．

解答 解：根据题意得出A的运动曲线，
当x=$\sqrt{2}$时，f（x）最大值$\sqrt{2}$，
根据图形判断①正确，
根据图形的重复性可得出：f（x）是周期函数且周期为2+$\sqrt{2}$；
故②不正确，
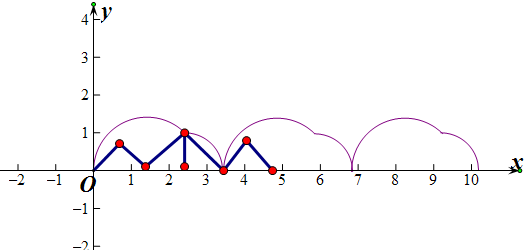
根据函数图象的单调性可得出f（x）的一个减区间是[$\sqrt{2}$，$\sqrt{2}$+2]；
故③正确，
④${∫}_{0}^{\sqrt{2}+1}$f（x）dx=$\frac{3}{4}$×$\frac{1}{2}×π×（\sqrt{2}）$²$+\frac{1}{2}×1×1$=$\frac{3}{4}$π$+\frac{1}{2}$=$\frac{3π}{4}$+$\frac{1}{2}$；
故④正确，
∵f（1）=$\sqrt{2\sqrt{2}-1}$＞1，f（$\sqrt{2}+1$）=1，
f（100$+51\sqrt{2}$）=f（$\sqrt{2}$）=$\sqrt{2}$，
∴f（100$+51\sqrt{2}$）＞f（1）＞＞f（$\sqrt{2}+1$），
故④不正确，
故答案为：①③④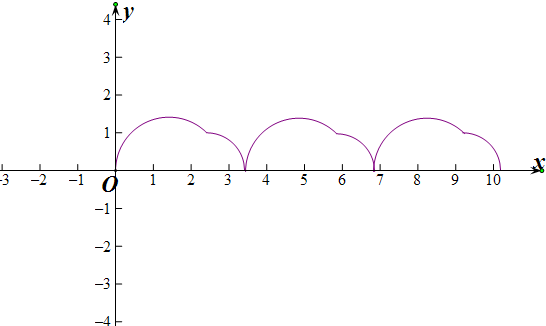

点评 本题是一道很有难度的题目，仔细阅读题意，得出动点的运动规律，画出图形，逐一判断即可．