
分析 由已知结论可得f(x)的对称中心为($\frac{1}{2}$,-1),即有f(x)+f(1-x)=-2,此数列前2017项的和按正常顺序写一遍,再倒过来写,即运用数列的求和方法:倒序球和法,化简即可得到所求和.
解答 解:若函数f(x)的表达式为f(x)=$\frac{ax+b}{cx+d}$ (c≠0),
则函数f(x)的图象的对称中心为(-$\frac{d}{c}$,$\frac{a}{c}$),
现已知函数f(x)=$\frac{2-2x}{2x-1}$,则对称中心为($\frac{1}{2}$,-1),
即有f(x)+f(1-x)=-2,
则数列前2017项的和为S2017=f($\frac{1}{2017}$)+f($\frac{2}{2017}$)+…+f($\frac{2016}{2017}$)+f(1),
则S2017=f($\frac{2016}{2017}$)+f($\frac{2015}{2017}$)+…+f($\frac{1}{2017}$)+f(1),
相加可得2S2017=[f($\frac{1}{2017}$)+f($\frac{2016}{2017}$)]+[f($\frac{2}{2017}$)+f($\frac{2015}{2017}$)]+…+2f(1)
=-2+(-2)+…+(-2)+0=-2×2016,
则此数列前2017项的和为-2016.
故答案为:-2016.
点评 本题考查函数的对称性及应用,考查数列的求和方法:倒序相加求和,考查运算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
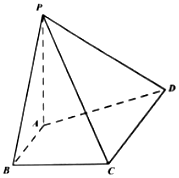 在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | ac>bc | C. | loga(a-c)>logb(b-c) | D. | $\frac{a}{a-c}$>$\frac{b}{b-c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
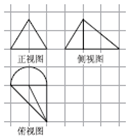 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )| A. | 1+$\frac{2π}{3}$ | B. | $\frac{4}{3}$+$\frac{2π}{3}$ | C. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{6}$ | D. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
已知向量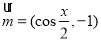 ,
,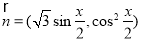 ,函数
,函数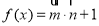 .
.
(1)若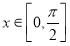 ,
,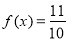 ,求
,求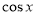 的值;
的值;
(2)在△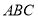 中,角
中,角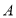 ,
,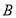 ,
,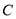 的对边分别是
的对边分别是 ,
,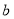 ,
,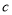 ,且满足
,且满足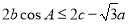 ,求角
,求角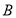 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\frac{\sqrt{85}}{2}$ | D. | $\frac{85}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com