
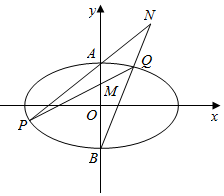
 ��ƽ��ֱ������ϵxOy�У���֪A��B�ֱ�����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ϡ��¶��㣬��M��0��$\frac{1}{2}$��Ϊ�߶�AO���е㣬AB=$\sqrt{2}$a��
��ƽ��ֱ������ϵxOy�У���֪A��B�ֱ�����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ϡ��¶��㣬��M��0��$\frac{1}{2}$��Ϊ�߶�AO���е㣬AB=$\sqrt{2}$a������ ��1��������֪2b=4��b-$\frac{1}{2}$��=$\sqrt{2}a$���ɴ��������Բ�ķ��̣�
��2������N��t��2����A��0��1����B��0��-1������ֱ��NA�ķ���Ϊy=$\frac{1}{t}x+1$��ֱ��NB�ķ���Ϊ$y=\frac{3}{t}x-1$���������������P��-$\frac{4t}{{t}^{2}+2}$��$\frac{{t}^{2}-2}{{t}^{2}+2}$����Q��$\frac{12t}{{t}^{2}+18}$��$\frac{18-{t}^{2}}{{t}^{2}+18}$�����Ӷ�kPM=kQM���ɴ���֤��P��M��Q���㹲�ߣ�
����${k}_{1}=\frac{1}{t}$��${k}_{2}=\frac{1}{3t}$��${k}_{3}=\frac{6-{t}^{2}}{8t}$����֤��k1k3+k2k3-k1k2Ϊ��ֵ��
��� �⣺��1����A��B�ֱ�����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ϡ��¶��㣬��M��0��$\frac{1}{2}$��Ϊ�߶�AO���е㣬AB=$\sqrt{2}$a��
��������֪2b=4��b-$\frac{1}{2}$��=$\sqrt{2}a$��
���a=$\sqrt{2}$��b=1��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{2}+{y}^{2}=1$��
֤������2������N��t��2����A��0��1����B��0��-1����
��ֱ��NA�ķ���Ϊy=$\frac{1}{t}x+1$��
ֱ��NB�ķ���Ϊ$y=\frac{3}{t}x-1$��
��$\left\{\begin{array}{l}{y=\frac{1}{t}x+1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-\frac{4t}{{t}^{2}+2}}\\{y=\frac{{t}^{2}-2}{{t}^{2}+2}}\end{array}\right.$����P��-$\frac{4t}{{t}^{2}+2}$��$\frac{{t}^{2}-2}{{t}^{2}+2}$����
��$\left\{\begin{array}{l}{y=\frac{3}{t}x-1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{12t}{{t}^{2}+18}}\\{y=\frac{18-{t}^{2}}{{t}^{2}+18}}\end{array}\right.$����Q��$\frac{12t}{{t}^{2}+18}$��$\frac{18-{t}^{2}}{{t}^{2}+18}$����
ֱ��PM��б��kPM=$\frac{\frac{{t}^{2}-2}{{t}^{2}+2}-\frac{1}{2}}{-\frac{4t}{{t}^{2}+2}}$=$\frac{6-{t}^{2}}{8t}$��
ֱ��QM��б��kQM=$\frac{\frac{18-{t}^{2}}{{t}^{2}+18}-\frac{1}{2}}{\frac{12t}{{t}^{2}+18}}$=$\frac{6-{t}^{2}}{8t}$��
��kPM=kQM����P��M��Q���㹲�ߣ�
���ɢ�֪��${k}_{1}=\frac{1}{t}$��${k}_{2}=\frac{1}{3t}$��${k}_{3}=\frac{6-{t}^{2}}{8t}$��
��k1k3+k2k3-k1k2=$\frac{4}{t}��\frac{6-{t}^{2}}{8t}$-$\frac{3}{{t}^{2}}$=-$\frac{1}{2}$��
��k1k3+k2k3-k1k2Ϊ��ֵ-$\frac{1}{2}$��
���� ���⿼����Բ���̵����������㹲�ߵ�֤�����������ʽ�ĺ�Ϊ��ֵ��֤�������е��⣬����ʱҪ�������⣬ע����Բ���ʡ�ֱ�߷��̵ĺ������ã�


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��2��0�� | C�� | ��0��-2�� | D�� | ��-2��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����f��x��=Asin��x��A��0���أ�0���IJ���ͼ����ͼ��ʾ��f��1��+f��2��+f��3��+��+f��2016����ֵΪ��������
����f��x��=Asin��x��A��0���أ�0���IJ���ͼ����ͼ��ʾ��f��1��+f��2��+f��3��+��+f��2016����ֵΪ��������| A�� | 0 | B�� | 3$\sqrt{2}$ | C�� | 6$\sqrt{2}$ | D�� | -$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $-\frac{\sqrt{3}}{2}$ | C�� | cos50�� | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com