
分析 由${V}_{A-{A}_{1}EF}={V}_{E-{A}_{1}AF}$,能求出三棱锥A-A1EF的体积.
解答 解:∵${V}_{A-{A}_{1}EF}={V}_{E-{A}_{1}AF}$,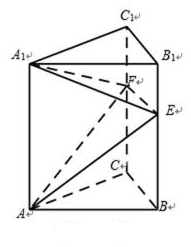 过B1作B1D⊥A1C1,
过B1作B1D⊥A1C1,
∵正三棱柱ABC-A1B1C1,
∴B1D⊥A1A,即B1D⊥面AA1C1C,
在△A1B1C1中,B1D=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵B1B∥面A1ACC1,
∴E点到面AA1C1C的距离等于B1到面AA1C1C的距离,
∴三棱锥A-A1EF的体积:
${V}_{A-{A}_{1}EF}={V}_{E-{A}_{1}AF}$=$\frac{1}{3}×\frac{1}{2}×6×4×2\sqrt{3}$=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$.
点评 本题考查考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想、数形结合思想,是中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150种 | B. | 90种 | C. | 60种 | D. | 180种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
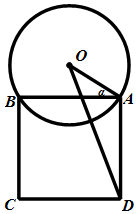 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com