
分析 根据超级囧函数的定义,分别判断函数是否满足条件即可得到结论.
解答 解:对于(1)不满足①对任意的x∈[0,+∞),总有f(x)≥0,故(1)不是超级囧函数;
对于(2),g(x)=$\frac{1}{4}{x^2}$(x∈[0,1]),则g(x1+x2),g(x+1)可能没意义,故故(2)不是超级囧函数;
对于(3),函数h(x)=2x-1(x∈[0,+∞)上满足h(x)≥0,
若x1≥0,x2≥0,x1+x2≤1,则h(x1+x2)-[h(x1)+h(x2)]=2x1+x2-1-[(2x1-1)+(2x2-1)
=2x1+x2-2x1-2x2+1)=(2x1-1)(2x2-1)≥0,
即h(x1+x2)≥h(x1)+h(x2),
要满足0≤x1<x2<1,则$\frac{{f({x_1}+1)-f({x_2}+1)}}{{{x_1}-{x_2}}}$>1,只需f(x1+1)-f(x2-1)<(x1+1)-(x2+1),即函数G(t)=f(t)-t在[1,2)上递增即可.函数h(x)=2x-1显然满足,故(3)是超级囧函数;
对于(4),x1≥0,x2≥0时,p(x1+x2)-[p(x1)+p(x2)]=ln$\frac{{x}_{1}+{x}_{2}+1}{{(x}_{1}+1)({x}_{2}+1)}$=ln$\frac{{x}_{1}+{x}_{2}+1}{{x}_{1}+{x}_{2}+{x}_{1}{x}_{2}+1}$≤0,故不满足②若x1≥0,x2≥0,都有f(x1+x2)≥f(x1)+f(x2)成立,故(4)不是超级囧函数;
故答案为:(3)
点评 本题主要考查抽象函数的应用,根据函数的定义分别判断条件已经利用赋值法是解决抽象函数的基本方法.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\{\left.x\right|-2≤x<\frac{3}{2}\}$ | B. | {x|x<2} | C. | $\{\left.x\right|-2<x<\frac{3}{2}\}$ | D. | {x|x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当$q=\frac{1}{2}$时,方程组有无穷多解 | |
| D. | 当且仅当$q=\frac{1}{2}$时,方程组无解 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
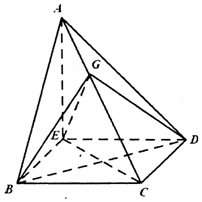 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 65 | C. | 80 | D. | 81 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com