
分析 根据f(x)为奇函数,设x>0,得-x<0,可求出f(x)=e-x(x-1)判定①正确;
由f(x)解析式求出-1,1,0都是f(x)的零点,判定②错误;
由f(x)解析式求出f(x)>0的解集,判断③正确;
分别对x<0和x>0时的f(x)求导,根据导数符号判断f(x)的单调性,
根据单调性求f(x)的值域,可得?x1,x2∈R,有|f(x1)-f(x2)|<2,判定④正确.
解答 解:对于①,f(x)为R上的奇函数,设x>0,则-x<0,
∴f(-x)=e-x(-x+1)=-f(x),∴f(x)=e-x(x-1),①正确;
对于②,∵f(-1)=0,f(1)=0,且f(0)=0,
∴f(x)有3个零点,②错误;
对于③,x<0时,f(x)=ex(x+1),易得x<-1时,f(x)<0;
x>0时,f(x)=e-x(x-1),易得0<x<1时,f(x)<0;
∴f(x)<0的解集为(-∞,-1)∪(0,1);③正确;
对于④,x<0时,f′(x)=ex(x+2),得
x<-2时,f′(x)<0,-2<x<0时,f′(x)>0;
∴f(x)在(-∞,0)上单调递减,在(-2,0)上单调递增;
∴x=-2时,f(x)取最小值-e-2,且x<-2时,f(x)<0;
∴f(x)<f(0)=1;
即-e-2<f(x)<1;
x>0时,f′(x)=e-x(2-x);
∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减;
x=2时,f(x)取最大值e-2,且x>2时,f(x)>0;
∴f(x)>f(0)=-1;
∴-1<f(x)≤e-2;
∴f(x)的值域为(-1,e-2]∪[-e-2,1);
∴?x1,x2∈R,都有|f(x1)-f(x2)|<2;④正确;
综上,正确的命题是①③④.
故答案为①③④.
点评 本题考查了奇函数的定义与应用问题,也考查了函数的零点以及不等式的解集、根据导数符号判断函数单调性和求函数最值、求函数值域的方法,是综合性题目.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
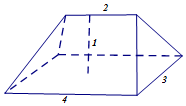 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).| A. | 5立方丈 | B. | 6立方丈 | C. | 7立方丈 | D. | 9立方丈 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{2}$-y2=1 | B. | x2-$\frac{{y}^{2}}{2}$=1 | C. | x2-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$-y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
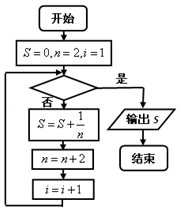
| A. | i>1009? | B. | i<1009? | C. | i>2018? | D. | i<2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 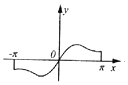 | C. | 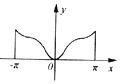 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com