
分析 设|PF2|=t,则|OF2|=|F2M|=$\frac{1}{2}$t=c,求得直线PF2的倾斜角为60°,由三角函数的定义,可得P(2c,$\sqrt{3}$c),代入双曲线的方程,运用a,b,c的关系和离心率公式,解方程即可得到所求值.
解答 解:设|PF2|=t,则|OF2|=|F2M|=$\frac{1}{2}$t=c,
即t=2c,由直线PF2的斜率为$\sqrt{3}$,可得
直线PF2的倾斜角为60°,
可得P(c+2ccos60°,2csin60°),
即为P(2c,$\sqrt{3}$c),代入双曲线的方程可得
$\frac{4{c}^{2}}{{a}^{2}}$-$\frac{3{c}^{2}}{{b}^{2}}$=1,
由b2=c2-a2,e=$\frac{c}{a}$,可得4e2-$\frac{3{e}^{2}}{{e}^{2}-1}$=1,
化为4e4-8e2+1=0,
解得e2=$\frac{4+2\sqrt{3}}{4}$($\frac{4-2\sqrt{3}}{4}$舍去),
即有e=$\frac{1+\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{3}+1}}{2}$.
点评 本题考查双曲线的离心率的求法,注意运用三角函数的定义和点满足双曲线的方程,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{3}$,+∞) | C. | (2,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
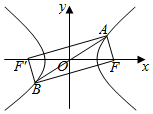 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )| A. | $[{\sqrt{2},\sqrt{3}+1}]$ | B. | $[{\sqrt{3},2+\sqrt{3}}]$ | C. | $[{\sqrt{2},2+\sqrt{3}}]$ | D. | $[{\sqrt{3},\sqrt{3}+1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{17}+4}{4}$ | B. | $\frac{\sqrt{17}+3}{4}$ | C. | $\frac{\sqrt{17}+2}{4}$ | D. | $\frac{\sqrt{17}+1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com