
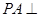 平面ABCD,AD//BC,
平面ABCD,AD//BC,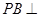 AC,
AC,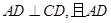
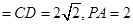 ,点M在线段PD上.
,点M在线段PD上.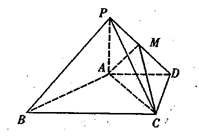
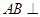 平面PAC;
平面PAC;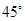 ,试确定点M的位置.
,试确定点M的位置. 为线段
为线段 的中点.
的中点.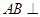 平面
平面 ,只要证:
,只要证: ,由题设
,由题设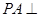 平面
平面
 ,结合条件
,结合条件 ,可证
,可证 平面
平面 ,从而有
,从而有 ,结论可证.
,结论可证. 为坐标原点,
为坐标原点, 分别为
分别为 轴,
轴, 轴,
轴, 轴建立空间直角坐标系
轴建立空间直角坐标系 如图所示
如图所示 和平面
和平面 的法向量,利用向量的夹角公式求出点
的法向量,利用向量的夹角公式求出点 的坐标,从而确定点M的位置.
的坐标,从而确定点M的位置.
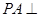 平面
平面 ,
, 平面
平面
 ,
, 2分
2分 ,
, ,
, 平面
平面 ,
, ,
, 平面
平面 3分
3分 平面
平面 ,
, 平面
平面 ,
,
 4分
4分
 ,
, ,
, 平面
平面 ,
, ,
,  平面
平面 6分
6分 ⊥平面
⊥平面 ,又由(1)知
,又由(1)知 ,
, .则
.则 ,
, ,
, ,
, ,
, ,
,
 ,
, ,则
,则  ,
, 坐标为
坐标为 ,
, 8分
8分 的法向量为
的法向量为 ,则
,则 9分
9分
 ,则
,则 . 10分
. 10分 的法向量
的法向量
 , 解得
, 解得
 为线段
为线段 的中点. 12分
的中点. 12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
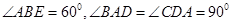 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.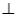 平面
平面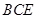 ;(2)点M在直线EF上,且
;(2)点M在直线EF上,且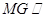 平面
平面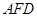 ,求平面ACH与平面ACM所成锐角的余弦值.
,求平面ACH与平面ACM所成锐角的余弦值.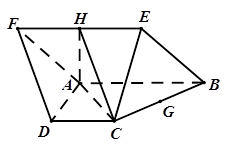
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点. 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 的位置,并说明理由;
的位置,并说明理由; ⊥A1C.
⊥A1C.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
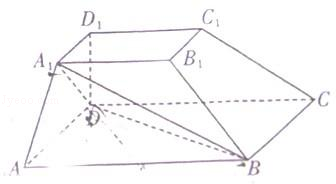
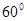 的菱形
的菱形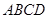 沿较短对角线
沿较短对角线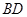 折成二面角
折成二面角 ,点
,点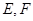 分别为
分别为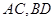 的中点,给出下列四个命题:
的中点,给出下列四个命题: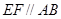 ;②
;②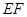 是异面直线
是异面直线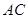 与
与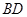 的公垂线;③当二面角
的公垂线;③当二面角 是直二面角时,
是直二面角时,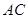 与
与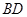 间的距离为
间的距离为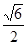 ;④
;④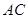 垂直于截面
垂直于截面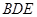 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
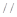 平面
平面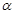 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面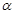 上的射影
上的射影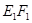 长的范围是( )
长的范围是( )A.[0, ] ] | B.[ , , ] ] |
C.[ , , ] ] | D.[ , , ] ] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com