
分析 (1)通过对函数f(x)=x-1-alnx(x>0)求导,分a≤0、a>0两种情况考虑导函数f′(x)与0的大小关系可得结论;
(2)通过(1)可知lnx≤x-1,进而取特殊值可知ln(1+$\frac{1}{{2}^{k}}$)<$\frac{1}{{2}^{k}}$,k∈N*.一方面利用等比数列的求和公式放缩可知(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)<e,另一方面可知(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)>2,从而当n≥3时,(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)∈(2,e),比较可得结论.
解答 解:(1)因为函数f(x)=x-1-alnx,x>0,
所以f′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,且f(1)=0.
所以当a≤0时f′(x)>0恒成立,此时y=f(x)在(0,+∞)上单调递增,这与f(x)≥0矛盾;
当a>0时令f′(x)=0,解得x=a,
所以y=f(x)在(0,a)上单调递减,在(a,+∞)上单调递增,即f(x)min=f(a),
又因为f(x)min=f(a)≥0,
所以a=1;
(2)由(1)可知当a=1时f(x)=x-1-lnx≥0,即lnx≤x-1,
所以ln(x+1)≤x当且仅当x=0时取等号,
所以ln(1+$\frac{1}{{2}^{k}}$)<$\frac{1}{{2}^{k}}$,k∈N*.
一方面,ln(1+$\frac{1}{2}$)+ln(1+$\frac{1}{{2}^{2}}$)+…+ln(1+$\frac{1}{{2}^{n}}$)<$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$<1,
即(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)<e;
另一方面,(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)>(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{3}}$)=$\frac{135}{64}$>2;
从而当n≥3时,(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)∈(2,e),
因为m为整数,且对于任意正整数n,(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)…(1+$\frac{1}{{2}^{n}}$)<m成立,
所以m的最小值为3.
点评 本题是一道关于函数与不等式的综合题,考查分类讨论的思想,考查转化与化归思想,考查运算求解能力,考查等比数列的求和公式,考查放缩法,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
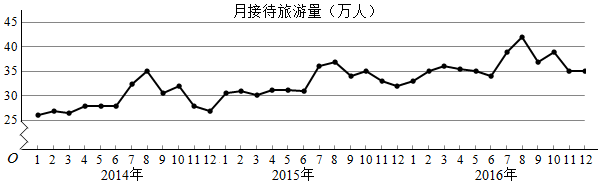
| A. | 月接待游客量逐月增加 | |
| B. | 年接待游客量逐年增加 | |
| C. | 各年的月接待游客量高峰期大致在7,8月 | |
| D. | 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1盏 | B. | 3盏 | C. | 5盏 | D. | 9盏 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com