
已知函数f(x)=x2·ln|x|(x≠0).
(1)求f(x)的最值;
(2)若关于x的方程f(x)=kx-1无实数解,求实数k的取值范围.
(1)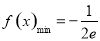 ;(2)
;(2)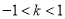 .
.
【解析】
试题分析:(1)由已知显然该函数是偶函数,所以只需研究当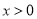 时的函数最值,由于函数是对数函数,可用导数法求最值,因此对函数求导,令
时的函数最值,由于函数是对数函数,可用导数法求最值,因此对函数求导,令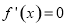 ,判断导数在定义域内的符号确定单调性,从而可得函数的最值;(2)由(1)作出函数
,判断导数在定义域内的符号确定单调性,从而可得函数的最值;(2)由(1)作出函数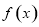 的图像,方程
的图像,方程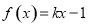 无实数解时,由图像可知,求出相切时
无实数解时,由图像可知,求出相切时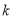 的值,结合图象可确定
的值,结合图象可确定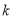 的范围.
的范围.
试题解析:(1)∵f(x)为偶函数,∴我们先求其在(0,+∞)内的最值.
求导得: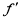 (x)=x(2lnx+1), 令
(x)=x(2lnx+1), 令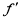 (x)=0 ⇒ 2lnx+1=0 ⇒ x=e
(x)=0 ⇒ 2lnx+1=0 ⇒ x=e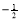 ,由此易知:
,由此易知:
x∈(0, e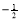 )时,
)时,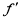 (x)<0 ⇒ f(x)单调递减;x∈(e
(x)<0 ⇒ f(x)单调递减;x∈(e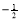 ,+∞)时,
,+∞)时,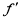 (x)>0 ⇒f(x)单调递增.
(x)>0 ⇒f(x)单调递增.
故f(x)在[0,+∞)上的最小值f(x)min=f(e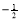 )=-
)=-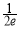 .
.
再由f(x)为偶函数,其图像关于y轴对称即知:f(x)min=-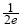 为所求.
为所求.
(2)由(1)知:f(x)的图像大致如右图所示,由图像知:当求出直线y=kx-1
与f(x)的图像相切时,其斜率k的值后,便可求得该直线与f(x)的图像无交点,即
方程f(x)=kx-1无实数解时,其斜率k的取值范围. 我们先考虑x>0的情况.
设切点为(x0, y0),x0>0⇒ k切=x0(2ln x0+1)⇒切线方程为:y=x0(2ln x0+1)x+y0-x02(2ln x0+1),
因该切线与y=kx-1重合,故x02(2ln x0+1)=1 ⇒2x02ln x0=1-x02 .此即2 f(x0) =1-x02.(※)
在同一坐标系内,作出函数y=2f(x), x>0, 与y=1-x2的图像,可知它们的交点为(1, 0).故方程(※)的解为:x0=1 ⇒k切=1;⇒x>0时,k≥1,直线y=kx-1与f(x)的图像有交点(即原方程有解).
再根据f(x)的图像的对称性易知:k≤-1时,直线y=kx-1与f(x)的图像也有交点.
故-1<k<1时,直线y=kx-1与f(x)的图像无交点,即方程f(x)=kx-1无实数解.

考点:利用导数研究函数的单调性、极值、等性质,确定函数的图象,方程根的取值.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
“ ”是“直线
”是“直线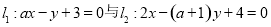 互相平行”的( )
互相平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:填空题
已知△ABC内部的一点O,恰使 +2
+2 +3
+3 =
=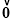 ,则△OAB,△OAC,△OBC的面积之比为_______________.(结果须化为最简)
,则△OAB,△OAC,△OBC的面积之比为_______________.(结果须化为最简)
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:选择题
已知△ABC的三内角A, B, C所对边的长依次为a,b,c,M为该三角形所在平面内的一点,若a +b
+b +c
+c =
= ,则M是△ABC的( )
,则M是△ABC的( )
A.内心 B.重心 C.垂心 D.外心
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修物理)(解析版) 题型:填空题
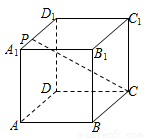
如图,已知点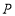 是正方体
是正方体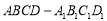 的棱
的棱 上的一个动点,设异面直线
上的一个动点,设异面直线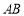 与
与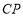 所成的角为
所成的角为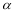 ,则
,则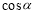 的最小值是 .
的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com