练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．如图，在△ABC中，已知∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，有下列结论：①四边形CEDF有可能成为正方形；②△DFE是等腰直角三角形；③四边形CEDF的面积是定值；④点C到线段EF的最大距离为$\sqrt{2}$．
    其中正确的结论是（　　）?
    A．①④B．②③C．①②④D．①②③④

    分析 ①当点E，F分别为AC，CB的中点时，四边形CEDF为正方形，即可判断出正误；
    ②如图所示，建立直角坐标系，设E（a，0），则F（0，4-a），D（2，2），于是$\overrightarrow{DF}$=（-2，2-a），$\overrightarrow{DE}$=（a-2，-2），计算$\overrightarrow{DF}•\overrightarrow{DE}$=0，可得$\overrightarrow{DE}⊥\overrightarrow{DF}$，又$|\overrightarrow{DE}|$=$|\overrightarrow{DF}|$=$\sqrt{（a-2）^{2}+4}$，即可判断出正误；
    ③四边形CEDF的面积=S△ABC-S△ADE-S△BDF=$\frac{1}{2}×{4}^{2}$-$\frac{1}{2}×AD×AEsin4{5}^{°}$-$\frac{1}{2}×BD×BFsin4{5}^{°}$，即可判断出正误；
    ④设点C到线段EF的距离为h，利用S△CEF=$\frac{1}{2}CE•CF$=$\frac{1}{2}h•EF$，可得$h=\frac{CE•CF}{\sqrt{C{E}^{2}+C{F}^{2}}}$，设CE=x，则CF=4-x，可得h=$\frac{4x-{x}^{2}}{\sqrt{2{x}^{2}-8x+16}}$，令4x-x2=t∈（0，4]，则h（x）=g（t）=$\frac{t}{\sqrt{16-2t}}$，g2（t）=$\frac{{t}^{2}}{16-2t}$=f（t），利用导数研究其单调性极值与最值，即可判断出正误．

    解答 解：①当点E，F分别为AC，CB的中点时，四边形CEDF为正方形，正确；
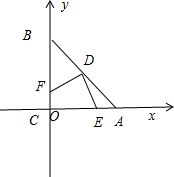
    ②如图所示，建立直角坐标系，设E（a，0），则F（0，4-a），D（2，2），于是$\overrightarrow{DF}$=（-2，2-a），$\overrightarrow{DE}$=（a-2，-2），
    ∴$\overrightarrow{DF}•\overrightarrow{DE}$=-2（a-2）-2（2-a）=0，∴$\overrightarrow{DE}⊥\overrightarrow{DF}$，又$|\overrightarrow{DE}|$=$|\overrightarrow{DF}|$=$\sqrt{（a-2）^{2}+4}$，因此△DFE可以是等腰直角三角形，正确；
    ③四边形CEDF的面积=S△ABC-S△ADE-S△BDF=$\frac{1}{2}×{4}^{2}$-$\frac{1}{2}×AD×AEsin4{5}^{°}$-$\frac{1}{2}×BD×BFsin4{5}^{°}$=8-$\frac{\sqrt{2}}{2}（AE+BF）$=$8-\frac{\sqrt{2}}{2}×4$=8-2$\sqrt{2}$是定值，因此正确；
    ④设点C到线段EF的距离为h，∵S△CEF=$\frac{1}{2}CE•CF$=$\frac{1}{2}h•EF$，∴$h=\frac{CE•CF}{\sqrt{C{E}^{2}+C{F}^{2}}}$，设CE=x，则CF=4-x，∴h=$\frac{x（4-x）}{\sqrt{{x}^{2}+（4-x）^{2}}}$=$\frac{4x-{x}^{2}}{\sqrt{2{x}^{2}-8x+16}}$，令4x-x2=t∈（0，4]，则h（x）=g（t）=$\frac{t}{\sqrt{16-2t}}$，g2（t）=$\frac{{t}^{2}}{16-2t}$=f（t），f′（t）=$\frac{2t（16-2t）-（-2）{t}^{2}}{（16-2t）^{2}}$=$\frac{2t（16-t）}{（16-2t）^{2}}$＞0，∴函数f（t）在t∈（0，4]上单调递增，∴f（t）max=f（4）=$\frac{16}{16-8}$=2，
    因此g（t）即h的最大值为$\sqrt{2}$，正确．
    故选：D．

    点评 本题考查了向量垂直与数量积的关系、等腰直角三角形的性质、三角形的面积计算公式、利用导数研究函数的单调性极值与最值，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．已知抛物线C：y2=4x，点M（-1，1），过C的焦点且斜率为k的直线与C交于A，B两点，若$\overrightarrow{MA}•\overrightarrow{MB}=0$，则实数k的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知等差数列{an}满足，a1+a2+a3=9，a2+a8=18．数列{bn}的前n和为Sn，且满足Sn=2bn-2．
    （Ⅰ）求数列{an}和{bn}的通项公式；
    （Ⅱ）数列{cn}满足${c_n}=\frac{a_n}{b_n}$，求数列{cn}的前n和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设函数f（x）=$sin（2x+\frac{π}{3}）$的图象为M，下面结论中正确的是（　　）
    A．图象M可由y=sin2x的图象向左平移$\frac{π}{6}$个单位得到
    B．函数f（x）的最小正周期是4π
    C．图象M关于直线x=$\frac{π}{3}$对称
    D．函数y=f（x）在区间$（-\frac{5π}{6}，\frac{π}{6}）$上是增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设A（x1，y1），B（x2，y2）是函数f（x）=$\frac{1}{2}+{log_2}\frac{x}{1-x}$的图象上任意两点，P是AB中点，且P的横坐标为$\frac{1}{2}$．
    （Ⅰ）求证：P点的纵坐标为定值；
    （Ⅱ）若Sn=$f（\frac{1}{n}）+f（\frac{2}{n}）+…+f（\frac{n-1}{n}）$，n∈N*，且n≥2，求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在菱形ABCD中，∠BAD=60°，AB=4，点F是对角线BD上的动点，则$\overrightarrow{AF}$•$\overrightarrow{BF}$的最小值是（　　）
    A．-3B．-2C．-$\frac{3}{2}$D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知命题p：“将函数y=sin（2x+θ）的图象沿x轴向右平移$\frac{π}{16}$个单位后，得到一个关于y轴对称的图象”，命题q“θ=kπ+$\frac{5π}{8}$（k∈Z）“，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数f（x）=x+1（0≤x≤1），g（x）=2x-$\frac{1}{2}$（x≥1），函数h（x）=$\left\{\begin{array}{l}{f（x），0≤x＜1}\\{g（x），x≥1}\end{array}\right.$，若方程h（x）-k=0，k∈[$\frac{3}{2}$，2）有两个不同的实根m，n（m＞n≥0），则n•g（m）的取值范围为（　　）
    A．[$\frac{3}{2}$，2）B．[$\frac{1}{4}$，2）C．[$\frac{3}{4}$，3]D．[$\frac{3}{4}$，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．求过点（3，-2）且与椭圆4x2+9y2=36有相同焦点的椭圆方程．

    查看答案和解析>>

    同步练习册答案