Question

3．在菱形ABCD中，∠BAD=60°，AB=4，点F是对角线BD上的动点，则$\overrightarrow{AF}$•$\overrightarrow{BF}$的最小值是（　　）

• A． -3
• B． -2
• C． -$\frac{3}{2}$
• D． -1

Answer 1

分析 运用几何图形结合向量的运用得出$\overrightarrow{AF}$•$\overrightarrow{BF}$=λ（λ-1）$\overrightarrow{BA}$²+（2λ²-λ）$\overrightarrow{BA}$$•\overrightarrow{BC}$+λ²$\overrightarrow{BC}$²=16λ²-8λ，0≤λ≤1，再运用二次函数的单调性求解即可得出最小值．

解答 解：∵菱形ABCD中，∠BAD=60°，AB=4，
∴根据几何图形得出$\overrightarrow{BA}$$+\overrightarrow{BC}$=$\overrightarrow{BD}$，$\overrightarrow{BA}$$•\overrightarrow{BC}$=4×4×（-$\frac{1}{2}$）=-8，
$\overrightarrow{BA}$²=$\overrightarrow{BC}$²=16
设$\overrightarrow{BF}$=λ$\overrightarrow{BD}$，$\overrightarrow{AF}$=$\overrightarrow{BF}$$-\overrightarrow{BA}$=（λ-1）$\overrightarrow{BA}$+$λ\overrightarrow{BC}$，
∴$\overrightarrow{AF}$•$\overrightarrow{BF}$=λ（λ-1）$\overrightarrow{BA}$²+（2λ²-λ）$\overrightarrow{BA}$$•\overrightarrow{BC}$+λ²$\overrightarrow{BC}$²=16λ²-8λ，0≤λ≤1
根据函数的单调性可判断；当$λ=\frac{1}{4}$时，16λ²-8λ的最小值为16×$\frac{1}{16}$$-8×\frac{1}{4}$=-1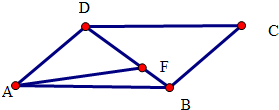

故选：D

点评 本题考查了平面向量的运用，转化为函数求解，关键是根据几何图形，运用数量积得出函数式子，属于中档题．