
分析 求出f′(x)=$\frac{1-2x}{{e}^{2x}}$,由此利用导数性质能求出函数f(x)=$\frac{x}{{e}^{2x}}$+1的最大值.
解答 解:∵f(x)=$\frac{x}{{e}^{2x}}$+1,
∴x∈R,f′(x)=$\frac{{e}^{2x}-2x{e}^{2x}}{({e}^{2x})^{2}}$=$\frac{1-2x}{{e}^{2x}}$,
由f′(x)=0,得1-2x=0,解得x=$\frac{1}{2}$,
当x∈(0,$\frac{1}{2}$)时,f′(x)>0;当x∈($\frac{1}{2},+∞$)时,f′(x)<0,
∴x=$\frac{1}{2}$时,函数f(x)=$\frac{x}{{e}^{2x}}$+1取最大值f($\frac{1}{2}$)=$\frac{\frac{1}{2}}{{e}^{2×\frac{1}{2}}}$+1=$\frac{1}{2e}+1$.
故答案为:$\frac{1}{2e}+1$.
点评 本题考查函数的最大值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
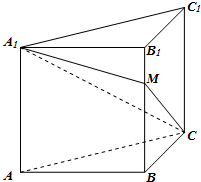 正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:将直角三角形PAO,绕直角边PO旋转构成圆锥,ABCD是⊙O的内接矩形,M为是母线PA的中点,PA=2AO.
如图:将直角三角形PAO,绕直角边PO旋转构成圆锥,ABCD是⊙O的内接矩形,M为是母线PA的中点,PA=2AO.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com