
| A. | [$\frac{5\sqrt{2}}{2}$-1,$\sqrt{34}+1$) | B. | [$\sqrt{17}-1$,$\sqrt{34}+1$] | C. | [$\sqrt{17}$,$\sqrt{34}$] | D. | [$\sqrt{17}$-1,$\sqrt{34}$-1] |
分析 首先求解平面区域的顶点,确定各顶点到圆心的距离$d=\sqrt{{{(x-5)}^2}+{y^2}}$,最后求出最小距离减半径和最大距离加半径,即为所求范围.
解答 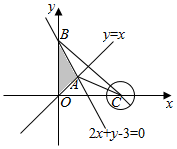 解:由约束条件$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 2x+y-3≤0\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 2x+y-3≤0\end{array}\right.$作出可行域如图,
O(0,0),B(0,3),
联立$\left\{\begin{array}{l}{y=x}\\{2x+y-3=0}\end{array}\right.$,解得A(1,1),
OC=5,AC=$\sqrt{(5-1)^{2}+(0-1)^{2}}=\sqrt{17}$,BC=$\sqrt{(5-0)^{2}+(0-3)^{2}}=\sqrt{34}$.
∴圆C:(x-5)2+y2=1上的点与区域D上的点之间的距离的最小值为$\sqrt{17}-1$,最大值为$\sqrt{34}+1$,
∴所求范围[$\sqrt{17}-1$,$\sqrt{34}+1$].
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,属于中档题型.


科目:高中数学 来源: 题型:解答题
| 逻辑思维能力 语言表达能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | m |
| 良好 | 4 | 4 | 1 |
| 优秀 | 1 | m | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 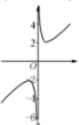 | B. | 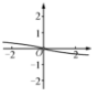 | C. |  | D. | 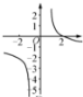 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
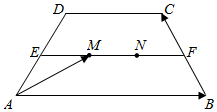 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
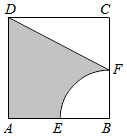 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com