
【题目】在直角坐标系中 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线 ![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)若直线 ![]() 与曲线
与曲线 ![]() 相交于点
相交于点 ![]() 两点,且
两点,且 ![]() ,求证:
,求证: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
【答案】
(1)
解:曲线 ![]() 的普通方程为
的普通方程为 ![]() ,
,
极坐标方程为 ![]() ,
,
∴所求的极坐标方程为 ![]() ;
;
(2)
不妨设设点 ![]() 的极坐标分别为
的极坐标分别为 ![]() ,
,
则 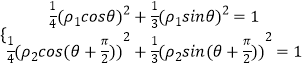 ,即
,即 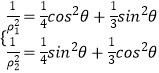 ,
,
∴ ![]() ,即
,即 ![]() (定值).
(定值).
【解析】(1)已知参数方程,根据cosθ+sinθ=1,有参数方程转化为普通方程;令
x= ![]() cosθ,y=
cosθ,y= ![]() sinθ,代入普通方程,即可得到极坐标方程。(2)用极坐标表示出A,B,将两个点代入方程即可。
sinθ,代入普通方程,即可得到极坐标方程。(2)用极坐标表示出A,B,将两个点代入方程即可。
【考点精析】利用参数方程的定义和椭圆的参数方程对题目进行判断即可得到答案,需要熟知在平面直角坐标系中,如果曲线上任意一点的坐标![]() 都是某个变数
都是某个变数![]() 的函数
的函数![]() 并且对于
并且对于![]() 的每一个允许值,由这个方程所确定的点
的每一个允许值,由这个方程所确定的点![]() 都在这条曲线上,那么这个方程就叫做这条曲线的参数方程;椭圆
都在这条曲线上,那么这个方程就叫做这条曲线的参数方程;椭圆![]()
![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知D为圆O:x2+y2=8上的动点,过点D向x轴作垂线DN,垂足为N,T在线段DN上且满足 ![]() .
.
(1)求动点T的轨迹方程;
(2)若M是直线l:x=﹣4上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(3)若(2)中直线PQ与动点T的轨迹交于G,H两点,且 ![]() ,求此时弦PQ的长度.
,求此时弦PQ的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ![]() .
.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点. (Ⅰ)求证:A1C1⊥AP;
(Ⅱ)求二面角P﹣AM﹣B的余弦值.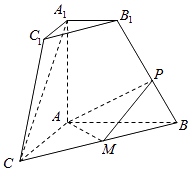
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷三枚不同的具有正、反两面的金属制品A1、A2、A3 , 假定A1正面向上的概率为 ![]() ,A2正面向上的概率为
,A2正面向上的概率为 ![]() ,A3正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设ξ表示正面向上的枚数.
,A3正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设ξ表示正面向上的枚数.
(1)求ξ的分布列及数学期望Eξ(用t表示);
(2)令an=(2n﹣1)cos( ![]() Eξ)(n∈N+),求数列{an}的前n项和.
Eξ)(n∈N+),求数列{an}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经十书,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com