
分析 a1=1,an+1=2an+1(n∈N*),变形为an+1+1=2(an+1),利用等比数列的通项公式可得:1+an,再利用等比数列的前n项和公式可得$\left\{{\frac{1}{{1+{a_n}}}}\right\}$的前n项和.
解答 解:a1=1,an+1=2an+1(n∈N*),
∴an+1+1=2(an+1),
∴数列{an+1}是等比数列,首项为2,公比为2.
∴1+an=2n,
∴$\frac{1}{1+{a}_{n}}$=$\frac{1}{{2}^{n}}$,
∴数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$的首项为$\frac{1}{2}$,公比为$\frac{1}{2}$.
∴数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$的各项和为:$\frac{\frac{1}{2}}{1-\frac{1}{2}}$=1.
故答案为:1.
点评 本题考查了等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3-2$\sqrt{2}$ | B. | 5-3$\sqrt{2}$ | C. | 9-6$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
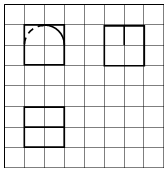 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )| A. | $6+\frac{π}{4}$ | B. | $6+\frac{π}{2}$ | C. | $6-\frac{π}{4}$ | D. | $6-\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
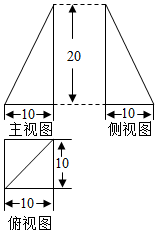 董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.
董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
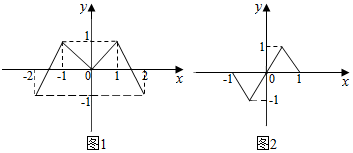 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )| A. | 3 | B. | 7 | C. | 10 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
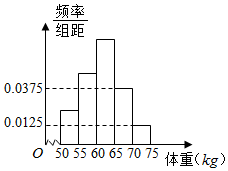 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com