
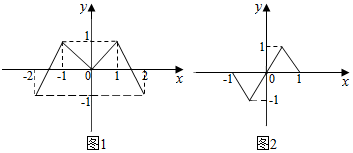 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,方程f(g(x))=0,g(f(x))=0的实根的个数分别为a,b,则a+b=( )| A. | 3 | B. | 7 | C. | 10 | D. | 14 |
分析 由f(x)和g(x)的图象便可看出f(g(x))=0时可得到g(x)=0,而由g(x)的图象即可看出g(x)=0的实根个数为3,从而便得出方程f(g(x))=0的实根个数a=3,而用同样的方法可以求出方程g(f(x))=0的实根个数b的值,从而得出a+b的值.
解答 解:由f(x),g(x)的图象和f(g(x))=0得:g(x)=0;
∴x=-1,0,1,即a=3;
由g(f(x))=0得,f(x)=0,-1,或1;
∴由f(x)的图象可看出f(x)=0的实根有3个,f(x)=-1的实根有2个,f(x)=1的实根有2个;
∴b=3+2+2=7;
∴a+b=10.
故选:C.
点评 考查奇函数、偶函数的定义,以及根据图象求方程实数根个数的方法,清楚函数f(x)的图象和x轴交点与方程f(x)=0实根的关系.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 4或8 | D. | 5或7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,| 轮次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲 | 73 | 66 | 82 | 72 | 63 | 76 |
| 乙 | 83 | 75 | 62 | 69 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种均有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com