
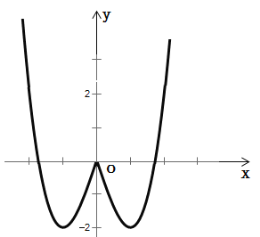
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的最大值;
的最大值;
(3)当![]() 时,求函数
时,求函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析(2)![]() (3)9个
(3)9个
【解析】
(1) 当![]() 时,
时,![]() 可得
可得![]() 是偶函数,当
是偶函数,当![]() 时,可得
时,可得![]() 是非奇非偶函数.
是非奇非偶函数.
(2) 当![]() 时,
时, ![]() ,即将问题转化为
,即将问题转化为![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,只要使
,只要使![]() .然后求出
.然后求出![]() 的导数,求出函数
的导数,求出函数![]() 的最小值.
的最小值.
(3)当![]() 时,
时,![]() ,得到
,得到![]() 得
得![]() 或
或![]() ,问题即求
,问题即求![]() 和
和![]() 和
和![]() 三个方程总的解的个数.
三个方程总的解的个数.
解:(1)函数定义域为![]() ,关于原点对称.
,关于原点对称.
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
则![]() 是定义在
是定义在![]() 上的偶函数;
上的偶函数;
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 且
且![]() ,
,
所以![]() 是非奇非偶函数.
是非奇非偶函数.
(2)当![]() 时,
时,![]() ,即已知
,即已知![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,只要使
,只要使![]() .
.
![]() ,因为
,因为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
即![]() 的最小值是
的最小值是![]() ,
,
解不等式![]() ,得
,得![]() .所以实数
.所以实数![]() 的最大值是
的最大值是![]() .
.
(3)当![]() 时,
时,![]() ,解
,解![]() 得
得![]() 或
或![]() ,
,
问题即求![]() 和
和![]() 和
和![]() 三个方程总的解的个数.
三个方程总的解的个数.
由(1)得函数![]() 是偶函数,
是偶函数,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,且
,且![]()
由偶函数的性质,![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
方程![]() 有3个解;方程
有3个解;方程![]() 有2个解;
有2个解;
方程![]() 有4个解;所以函数
有4个解;所以函数![]() 的零点个数是9个.
的零点个数是9个.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校![]() 名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表:
列联表:
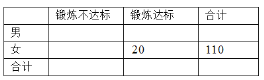
并通过计算判断,是否能在犯错误的概率不超过![]() 的前提下认为“锻炼达标”与性别有关?
的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出![]() 人,进行体育锻炼体会交流.
人,进行体育锻炼体会交流.
(i)求这![]() 人中,男生、女生各有多少人?
人中,男生、女生各有多少人?
(ii)从参加体会交流的![]() 人中,随机选出
人中,随机选出![]() 人发言,记这
人发言,记这![]() 人中女生的人数为
人中女生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: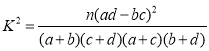 ,其中
,其中![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 |
0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
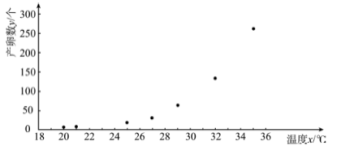
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
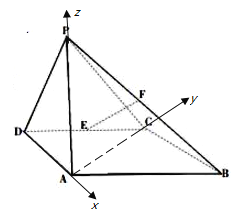
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种掷骰子走跳棋的游戏:棋盘上标有第0站、第1站、第2站、…、第100站,共101站,设棋子跳到第n站的概率为![]() ,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
(1)求![]() ,
,![]() ,
,![]() ,并根据棋子跳到第n站的情况,试用
,并根据棋子跳到第n站的情况,试用![]() 和
和![]() 表示
表示![]() ;
;
(2)求证:![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图,在五面体ABCDEF中,四边形EDCF是正方形,![]() .
.

(1)证明:![]() ;
;
(2)已知四边形ABCD是等腰梯形,且![]() ,求五面体ABCDEF的体积.
,求五面体ABCDEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com