
分析 (1)由已知得an+2=a(n+1)+b-an+1=(an+a+b)-(an+b)+an=a+an,由此能证明数列{an}是“弱等差数列”.由a1=t,a2=s,an+2-an=a,得到{an}中奇数项是以t为首项,以a为公差的等差数列,偶数列是以s为首项,以a为公差的等差数列,由此能求出数列{an}的通项公式.
(2)由递推公式求出a1=1,a2=3,a3=2a+b-3,a4=a+3,由此利用等差数列性质能求出a=4,b=0,从而得到数列{an}是首项为2,公差为2的等差数列,由此能求了Sn.
(3)由已知得a2k+1-a2k=(t+ka)-[s+(k-1)a]=t-s+a>0,由经能求出a的取值范围.
解答 证明:(1)∵数列{an}满足:a1=t,a2=s且an+an+1=an+b对于n∈N*恒成立,
∴an+1=an+b-an,
an+2=a(n+1)+b-an+1=(an+a+b)-(an+b)+an=a+an,
∴an+2-an=a,
∴数列{an}是“弱等差数列”.
∵a1=t,a2=s,an+2-an=a,
∴{an}中奇数项是以t为首项,以a为公差的等差数列,偶数列是以s为首项,以a为公差的等差数列,
∴an=$\left\{\begin{array}{l}{t+\frac{n-1}{2}a,n为奇数}\\{s+(\frac{n}{2}-1)a,n为偶数}\end{array}\right.$.
解:(2)∵当t=1,s=3时,数列{an}是等差数列,
∴a1=1,a2=3,3+a3=2a+b,
∴a3=2a+b-3,2a+b-3+a4=3a+b,∴a4=a+3,
∴$\left\{\begin{array}{l}{{a}_{3}-{a}_{2}=2a+b-3-3=2}\\{{a}_{4}-{a}_{3}=a+3-2a-b+3=2}\end{array}\right.$,解得a=4,b=0,
∴数列{an}是首项为2,公差为2的等差数列,
∴Sn=2n+$\frac{n(n-1)}{2}×2$=n2+n.
(3)∵s>t,且数列{an}是单调递增数列,
∴a2k+1-a2k=(t+ka)-[s+(k-1)a]=t-s+a>0,
∴a>s-t.
∴a的取值范围是(s-t,+∞).
点评 本题考查“弱等差数列”的证明,考查数列的通项公式的求法,综合性质强,难度大,解题时要认真审题,注意等差数列的性质的合理运用.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
已知函数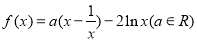 ,
,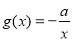 ,若至少存在一个
,若至少存在一个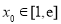 ,使
,使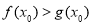 成立,则实数a的范围为( )
成立,则实数a的范围为( )
A.[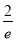 ,+∞) B.(0,+∞)
,+∞) B.(0,+∞)
C.[0,+∞) D.(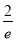 ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com