
分析 (Ⅰ)由f(x)的解析式得到最小值c-1,由|f(x)|-2=0有且只有两个不同的实根,得到不等式-2<c-1<2,由此得到c的取值范围.
(Ⅱ)由方程f(x)=x的两个实根为x1,x2,由韦达定理得到两个根的差的范围,用做差来判断两数的大小.
解答 解:(1)∵当a=1,b=2,∴f(x)=x2+2x+c=(x+1)2+c-1
∴-2<c-1<2
∴-1<c<3
(Ⅱ)方程f(x)=x,即ax2+(b-1)x+c=0,
由题意得${x_1}+{x_2}=\frac{1-b}{a},{x_1}{x_2}=\frac{c}{a}$,
$f(t)-{x_1}=a{t^2}+bt+c-(a{x_1}^2+b{x_1}+c)=(t-{x_1})(at+a{x_1}+b)$(1)
∵${x_1}+{x_2}=\frac{1-b}{a}$,
∴ax1+ax2=1-b,即ax1+b=1-ax2代入 (1)得
$f(t)-{x_1}=a{t^2}-bt+c-(a{x_1}^2-b{x_1}+c)=(t-{x_1})(at-a{x_2}+1)$
∵0<t<x1,∴t-x1<0,∵0<t<x1,
∴at-ax2+1<ax1-ax2+1,
∵${x_2}-{x_1}>\frac{1}{a}$,∴ax1-ax2<-1,即at-ax2+1<ax1-ax2+1<0.
所以f(t)>x1.
点评 本题考查由f(x)的解析式得到最小值,得到不等式-2<c-1<2,由此得到c的取值范围.由韦达定理得到两个根的差的范围,用做差来判断两数的大小.


科目:高中数学 来源: 题型:解答题
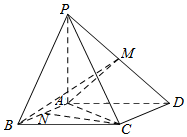 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 3$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若四边形不是菱形,则它的两条对角线不垂直 | |
| B. | 若四边形的两条对角线垂直,则它是菱形 | |
| C. | 若四边形的两条对角线垂直,则它不是菱形 | |
| D. | 若四边形是菱形,则它的两条对角线垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | 2 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com