
分析 根据函数单调性的定义利用定义法进行证明即可.
解答 解:任取x1,x2∈(0,+∞),且x1<x2,则$f({x_1})-f({x_2})=\frac{1}{{\sqrt{x_1}}}-\frac{1}{{\sqrt{x_2}}}$…(3分)
=$\frac{{\sqrt{x_2}-\sqrt{x_1}}}{{\sqrt{x_1}•\sqrt{x_2}}}=\frac{{({\sqrt{x_2}-\sqrt{x_1}})({\sqrt{x_2}+\sqrt{x_1}})}}{{\sqrt{x_1}•\sqrt{x_2}({\sqrt{x_2}+\sqrt{x_1}})}}$=$\frac{{{x_2}-{x_1}}}{{\sqrt{x_1}•\sqrt{x_2}({\sqrt{x_1}+\sqrt{x_2}})}}$…(6分)
因为x2-x1>0,$\sqrt{x_1}>0,\sqrt{x_2}>0$,
所以$\sqrt{x_1}+\sqrt{x_2}>0$,$\sqrt{x_1}•\sqrt{x_2}({\sqrt{x_1}+\sqrt{x_2}})>0$,…(8分)
所以f(x1)-f(x2)>0,
即函数$f(x)=\frac{1}{{\sqrt{x}}}$在区间(0,+∞)上是减函数.…(10分)
点评 本题主要考查函数单调性的判断,利用函数单调性的定义是解决本题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
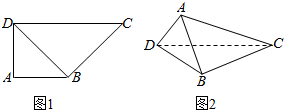 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com