考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据条件M={1},a
1=
,a
2=3
,求出数列数列的公比,即可求数列{a
n}的前n项和;
(2)根据条件M={3,4},a
1=
,判定数列为等比数列,即可求数列{a
n}的通项公式.
解答:
解:(1)当n≥2时,因为M={1},所以
=T
nT
1,可得a
n+1=a
na
1,故
=a
1=3(n≥2).
又a
1=
,a
2=3
,则{a
n}是公比为3的等比数列,
故{a
n}的前n项和为
=
•3
n-
.
(2)当n>k时,因为
=T
nT
k,所以
=T
n+1T
k,
所以
=
,即
=a
n+1,
因为M={3,4},所以取k=3,当n>3时,有a
n+4a
n-2=a
n+12;
取k=4,当n>4时,有a
n+5a
n-3=a
n+12.
由a
n+5a
n-3=a
n+12 知,
数列a
2,a
6,a
10,a
14,a
18,a
22,…,a
4n-2,…,是等比数列,设公比为q.…①
由a
n+4a
n-2=a
n+1 知,
数列a
2,a
5,a
8,a
11,a
14,a
17,…,a
3n-1,…,是等比数列,设公比为q
1,…②
数列a
3,a
6,a
9,a
12,a
15,a
18,…,a
3n,…,成等比数列,设公比为q
2,…③
数列a
4,a
7,a
10,a
13,a
16,a
19,a
22,…,a
3n+1,…,成等比数列,设公比为q
3,…④
由①②得,
=q
3,且
=q
14,所以q
1=q
;
由①③得,
=q
3,且
=q
24,所以q
2=q
;
由①④得,
=q
3,且
=q
34,所以q
3=q
;
所以q
1=q
2=q
3=q
.
由①③得,a
6=a
2q,a
6=a
3q
2,所以
=
=q
,
由①④得,a
10=a
2q
2,a
10=a
4q
32,所以
=
=q,
所以a
2,a
3,a
4是公比为q
的等比数列,所以{a
n}(n≥2)是公比为q
的等比数列.
因为当n=4,k=3时,T
7T
1=T
42T
32;
当n=5,k=4时,T
9T
1=T
52T
42,
所以(q
)
7=2a
24,且(q
)
10=2a
26,所以q
=2,a
2=2
.
又a
1=
,所以{a
n}(n∈N*)是公比为q
的等比数列.
故数列{a
n}的通项公式是a
n=2
n-1•
.
点评:本题主要考查等比数列的性质,考查运算能力、推理论证能力、分分类讨论等数学思想方法.综合性较强,难度较大.



 智能训练练测考系列答案
智能训练练测考系列答案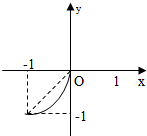 已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )
已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )