
分析 把圆C、直线l的极坐标方程都化为普通方程;求出圆心C到直线l的距离,利用勾股定理求出弦长AB的值.
解答 解:∵圆C的方程为ρ=4$\sqrt{2}$cos(θ-$\frac{π}{4}$),
∴ρ=4cosθ+4sinθ,
两边同乘以ρ,得:
ρ2=4ρcosθ+4ρsinθ,
∴普通方程为x2+y2-4x-4y=0,
其圆心C的坐标为(2,2),半径r=2$\sqrt{2}$;
又直线l的方程为ρsin($\frac{π}{4}$-θ)=$\sqrt{2}$,
化为普通方程是x-y-2=0;
∴圆心C到直线l的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴弦长AB=2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{8-2}$=2$\sqrt{6}$.
点评 本题考查了极坐标方程化为普通方程的应用问题,也考查了直线与圆的应用问题,是基础题目.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
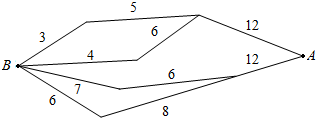 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | [1,5) | C. | {1,3,5} | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com